基本介紹
二次互反律

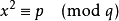

三次互反律
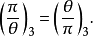
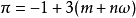


參見
- 二次互反律的證明
- 阿廷互反律


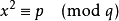

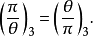
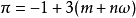


互反律可能是指:二次互反律或三次互反律。在數論中,特別是在同餘理論里,二次互反律(Law of Quadratic Reciprocity)是一個用於判別二次剩餘,即二次同餘方程之...
互反性是皮亞傑認知發展階段理論中的概念,屬於皮亞傑提出的“INRC群”里的成分。皮亞傑認為通過運用這一組中的成分可以獲得對一個問題的所有轉換。...
互反方程(reciprocal equation)是一種特殊的代數方程。代數方程理論的另一個問題是“一個方程能有多少個根”。中世紀阿拉伯和印度的數學家們都已認識到二次方程有...
正互反矩陣正互反矩陣的定義 編輯 若矩陣A=(aij)mxn滿足以下特徵:(1) aij>0(2)aij=1/aji則稱矩陣A 為正互反矩陣。V百科往期回顧 詞條統計 瀏覽次數:次...
在數學中,三次互反律是關於模代數中兩個對應的三次方程的可解性之間的關係的結論和定理。...
弗羅貝尼烏斯互反律(Frobenius reciprocity)在特徵標計算中將誘導特徵標與限制特徵標聯繫起來的重要公式.設X}}是群G的兩個復特徵標,定義X與必的內積 ...
戴德金互反律是和戴德金數相關的一種恆等式。 設p,q是互素的正整數,s(p,q) 是戴德金數。我們有 s(p,q)+s(q,p)=(p^2+q^2+1)/(12pq)-1/4....
只有到具體運算思維階段才形成發展起來。在具體運算思維階段,可逆性思維的逆向性和互反性是孤立出現的,到了形式運算思維階段,兩者已綜合成一個有機整體。...
勒讓德符號,或二次特徵,是一個由阿德里安-馬里·勒讓德在1798年嘗試證明二次互反律時引入的函式。這個符號是許多高次剩餘符號的原型;其它延伸和推廣包括雅可比...
只有到具體運算思維階段才形成發展起來。在具體運算思維階段,可逆性思維的逆向性和互反性是孤立出現的,到了形式運算思維階段,兩者已綜合成一個有機整體。...
序列反演(inversion of sequences)亦稱級數反演,是一對序列或級數可以相互表示的互反關係,聯繫這種互反關係的公式稱為反演公式。...
互滴法是一種鑑別物質的方法,可用於不用其他試劑鑑別一組物質。...... 互滴法是一種鑑別物質的方法,可用於不用...無明顯現象 反之,向Na2CO3溶液中滴入鹽酸...
我們可以二次互反律之推廣阿廷互反律為朗蘭茲綱領之起點: 給定一個Q上的、伽羅瓦群為可交換群的數域,阿廷互反律向這個伽羅瓦群的任何一支一維表示配上一枚L...
並用群論的術語與方法來給出關於有限與無限阿貝爾群的必要定理,導致了形式上與概念上相當的簡化;給出了任意代數數域中最一般二次互反律一個新的證明,並給出了...
全書共有三個核心課題:同餘理論、齊式論及剩餘論和二次互反律。這些都是高斯貢獻給數論的卓越成就。同餘理論同餘是《算術研究》中的一個基本研究課題。這個概念不...
