依次連線任意一個四邊形各邊中點所得的四邊形叫做中點四邊形。中點四邊形的形狀與原四邊形的對角線的數量和位置關係有關。
注意:對於對角線互相垂直的四邊形,連線各邊中點所得的四邊形一定是矩形。
矩形的判定方法:
1.有一個角是直角的平行四邊形是矩形 2.對角線相等的平行四邊形是矩形 3.有三個角是直角的四邊形是矩形
基本介紹
- 中文名:中點四邊形
- 套用學科:數學
- 適用領域範圍:數學等
定義
和原圖形關係
形狀

周長
面積
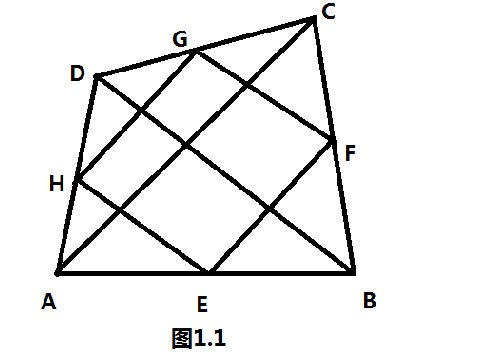 圖1.1
圖1.1

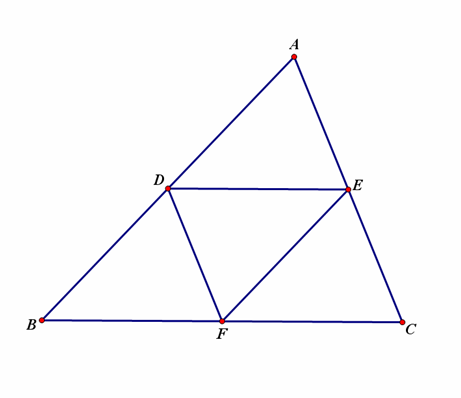 圖1.2
圖1.2





依次連線任意一個四邊形各邊中點所得的四邊形叫做中點四邊形。中點四邊形的形狀與原四邊形的對角線的數量和位置關係有關。
注意:對於對角線互相垂直的四邊形,連線各邊中點所得的四邊形一定是矩形。
矩形的判定方法:
1.有一個角是直角的平行四邊形是矩形 2.對角線相等的平行四邊形是矩形 3.有三個角是直角的四邊形是矩形

 圖1.1
圖1.1

 圖1.2
圖1.2




依次連線任意一個四邊形各邊中點所得的四邊形叫做中點四邊形。中點四邊形的形狀與原四邊形的對角線的數量和位置關係有關。注意:對於對角線互相垂直的四邊形,連線各...
由不在同一直線上的不交叉的四條線段依次首尾相接圍成的封閉的平面圖形或立體圖形叫四邊形,由凸四邊形和凹四邊形組成。順次連線任意四邊形上的中點所得四邊形叫...
由不在同一直線上四條線段依次首尾相接圍成的封閉的平面圖形或立體圖形叫四邊形,由凸四邊形和凹四邊形組成。...
在同一平面內,有一組鄰邊相等的平行四邊形是菱形,四邊都相等的四邊形是菱形,菱形的對角線互相垂直平分且平分每一組對角,菱形是軸對稱圖形,對稱軸有2條,即兩條...
8.對角線互相平分且有一個內角是直角的四邊形是矩形 依次連線四邊形各邊中點所得的四邊形稱為中點四邊形。不管原四邊形的形狀怎樣改變,中點四邊形的形狀始終是平行...
所以四邊形AECF的兩條對角線AC、EF互相平分且相等。故四邊形AECF為矩形。所以,當點O運動到AC的中點時,四邊形AECF是矩形。⑶在⑵中的矩形可能是正方形。...
2.5 四邊閉折線之舞//522.5.1 中點四邊形//522.5.2 牛頓線//542.6 雙圓四邊形//58習題//62第3章 星形折線與半多邊形//763.1 星形基本概念及性質//78...
題型三 中點四邊形 第三節 梯形中位線 題型一 計算 題型二 證明 綜合訓練 第八章 相似三角形 第一節 比例線段 題型一 計算 題型二 黃金分割 ...
平行四邊形的判定(複習)——“圖形與幾何”引導提問教學個案 測量池塘的寬度——“圖形與幾何”引導提問教學個案 與中點有關的四邊形問題——“圖形與幾何”引導...
二、“中點四邊形”問題的探究三、探究性活動——鑲嵌四、向量在物理中的套用五、二次函式在指定區間上的值域六、分類討論的3W原則...
“信息技術與學科整合”的展示課(徐玲玲老師的《出師表》,周建華老師的《中點四邊形》,孫堅崗老師的《我的父親母親(寫作指導)》,吳宜軍老師的《被子植物的有性繁殖...
活動1.13 奇妙的中點四邊形 活動1.14 相似三角形的套用 活動1.15 基本圖形在相似三角形中的作用 第二部分 活動2.01 構造有意義的圖案 活動2.02 探尋數學美 ...
中點四邊形 90 4.7.1 課件簡介 91 4.7.2 知識要點 91 4.7.3 製作步驟 91 4.8 驗證三角形的重心坐標公式 94 4.8.1 課件簡介 94 4.8.2 知識要點 94 4.8....
第21講中位線與中點四邊形 第22講函式中的動點問題(一) 第23講函式中的動點問題(二) 第24講一元二次方程的解法 第25講配方法 第26講一元二次方程...
No.4.5 中點四邊形No.4.6 中點四邊形性質探究詞條標籤: 出版物 , 書籍 圖集 新課標國中數學說課理論與實踐圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數...
