乘法公式

乘法公式（簡乘公式），將一些特殊的多項式相乘的結果加以總結，直接套用。公式中的每一個字母，一般可以表示數字，單項式，多項式，有的還可以推廣到分式，根式。乘法公式是整式乘法的重要內容,準確、熟練的掌握乘法公式對於學好整式乘法乃至整式的其他運算都有著重要的意義。乘法公式是最常用、最基礎的公式，可以由此而推導出其它公式。

其中大多數公式不僅可順用（多項式乘法），還可逆用（因式分解)。

基本介紹

• 中文名：乘法公式
• 別稱：簡乘公式
• 套用學科：數學，代數
• 舉例：完全平方公式及其變式

公式

• 完全平方公式及其變式。即

變式。即

• 平方差公式。即

• 立方和（差）公式。即

• 完全立方公式及其變式。即

變式。即

• 三數和平方公式。即

• 多項式平方公式。即（對於四項而言）

更高項的公式，用語言表述即：多項式的平方等於各項的平方和，加上每兩項積的2倍。

• 歐拉公式。即

• 平方和（差）、立方和（差）的一般情況即二項式定理。即

• 平方差、立方和公式的一般情況及其推論。即

設 為正整數，

類似地，

推論。當n為正整數時， 能被 整除； 能被 整除； 能被 及 整除。這是不難看出的。當然，這不在乘法公式的範圍之內。

例題

計算

I.（i） ；

（ii） ；

（iii）

分析。對於第（i）題，相乘的兩個二項式，只要它們有一項完全相同，另一項互為相反數，就符合平方差公式.相乘的結果是相同項的平方減去相反項的平方。第（i）題的相同項是2b，相反項是3a與－3a。

第（ii）題可以按第（i）題的方法計算，也可以先改變第二個因式的符號再運算。

第（iii）題雖然不能直接運用平方差公式計算，但認真觀察兩個二項式中的相同項和相反項，就不難分組轉化成平方差公式的結構形式。

解答。（i）原式

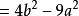
（ii）原式

（iii）原式

II.己知 ， 。求（i） ；（ii） ；（iii） ；（iv） 。

解答。（i） 。

（ii） 。

（iii） 。

（iv）

。

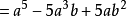
證明

I.求證。四個連續整數的積加上1的和，一定是整數的平方。

證明。設這四個數分別為 、 、 、 。（ 為整數）

。

∵ 是整數，整數的和，差，積，冪也是整數。∴ 是整數。

II.求證。 能被7整除。

證明。 。

∵ 能被a+b整除，

∴ 能被4+3整除。

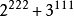∴ 能被7整除。