菱形

在同一平面內，有一組鄰邊相等的平行四邊形是菱形，四邊都相等的四邊形是菱形，菱形的對角線互相垂直平分且平分每一組對角，菱形是軸對稱圖形，對稱軸有2條，即兩條對角線所在直線，菱形是中心對稱圖形。

基本介紹

• 中文名：菱形
• 外文名：diamond，rhombus
• 拼寫：ling xing
• 所屬領域：數學幾何
• 本質：平行四邊形，特殊的箏形
• 特點：四邊相等，對角相等

定義

菱形（rhombus）是特殊的平行四邊形之一。有一組鄰邊相等的平行四邊形稱為菱形。如右圖，在平行四邊形ABCD中，若AB=BC，則稱這個平行四邊形ABCD是菱形，記作◇ABCD，讀作菱形ABCD。

性質

在一個平面內，有一組鄰邊相等的平行四邊形是菱形（rhombus）。

性質：

1. 菱形具有平行四邊形的一切性質；
2. 菱形的四條邊都相等；
3. 菱形的對角線互相垂直平分且平分每一組對角；
4. 菱形是軸對稱圖形，對稱軸有2條，即兩條對角線所在直線；
5. 菱形是中心對稱圖形；

判定

在同一平面內，

1. 一組鄰邊相等的平行四邊形是菱形；
2. 對角線互相垂直的平行四邊形是菱形；
3. 四條邊均相等的四邊形是菱形；
4. 對角線互相垂直平分的四邊形；
5. 兩條對角線分別平分每組對角的四邊形；
6. 有一對角線平分一個內角的平行四邊形；

菱形是在平行四邊形的前提下定義的，首先它是平行四邊形，而且是特殊的平行四邊形，特殊之處就是“有一組鄰邊相等”，因而增加了一些特殊的性質和判定方法。

菱形的一條對角線必須與x軸平行，另一條對角線與y軸平行。不滿足此條件的幾何學菱形在計算機圖形學上被視作一般四邊形。

面積

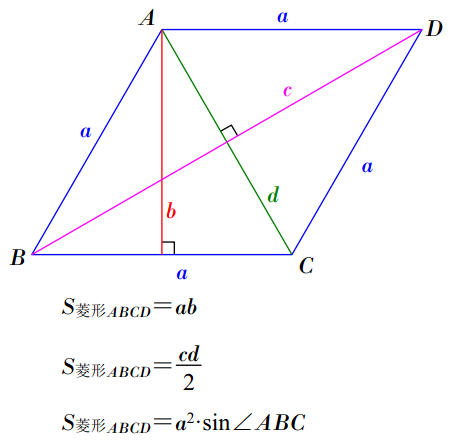
設一個菱形的面積為S，邊長為a，高為b，兩對角線分別為c和d，一個最小的內角為∠θ，則有：

1. S=ab（菱形和其他平行四邊形的面積等於底乘以高）；
2. S=cd÷2（菱形和其他對角線互相垂直的四邊形的面積等於兩對角線乘積的一半）；
3. S=a^2·sinθ。

中點四邊形

依次連線四邊形各邊中點所得的四邊形稱為中點四邊形。不管原四邊形的形狀怎樣，中點四邊形的形狀總是平行四邊形。

菱形的面積計算

菱形的中點四邊形總是矩形。（對角線垂直的四邊形的中點四邊形均為矩形）

常見圖案

如三菱汽車的標誌、閘門、衣服架等。

常見的閘門樣式