三等分角線(Trisectrix)是可以用來三等分任意角的曲線。若只用標準的尺規作圖,不配合曲線或是有刻度的直尺,“三等分一個已知角”在歷史上已證明是尺規作圖所不能解決的問題,但僅用尺規作出某一個三角形,並作出各角的三等分角線是可以做到的。有許多的曲線可以作為三等分角的輔助,而進行三等分角的方式也各有不同。
基本介紹
- 中文名:三等分角線
- 外文名:Trisectrix
- 相關定理:莫勒定理
- 相關曲線:等分曲線
- 適用領域:數理科學
- 類型:數學名詞
定義,性質,相關曲線,
定義
三等分角線(Trisectrix)是可以用來三等分任意角的曲線。
性質
三角形有關角三等分線的交點構成的三角形有許多美妙的性質。
定理一:與任意△ABC每邊相鄰的每兩個優角相鄰的三等分線的反向延長線的交點構成正三角形,且其邊長為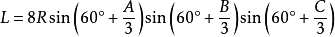 。
。
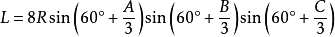
定理二:三角形任意一個優角與另兩個劣角中,與每邊相鄰的每兩個角相鄰的三等分線(或其反向延長線)的交點構成正三角形,且邊BC、AC、AB所正對的正三角形的邊長分別是:
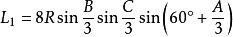


定理三:任意△ABC任意一邊相鄰的兩個優角相鄰三等分線的反向延長線的交點,及與這邊相鄰的劣角與外角相鄰的三等分線(或其反向延長線)的交點構成正三角形,且邊BC、AB、AC所正對的三角形的邊長分別是:


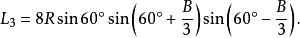
定理四:任意△ABC任意一邊相鄰的兩個外角相鄰三等分線的交點,及與這邊相鄰的劣角與優角相鄰三等分線(或其反向延長線)的交點構成正三角形,且點A、B、C所對的正三角形的邊長分別是:
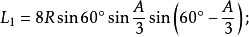


定理五:任意△ABC沒有公共頂點的任意一個劣角、一個優角及其夾邊所對的另兩個外角中,與每邊相鄰的每兩個角相鄰的三等分線(或其反向延長線)的交點構成正三角形,且六個正三角形的邊長分別是:


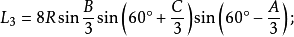

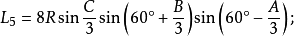
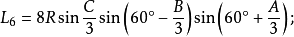
定理六:任意△ABC任意兩個優角及其夾邊所對的兩個外角中,與每邊相鄰的每兩個角相鄰的三等分線(或其反向延長線)的交點構成正三角形,且邊BC、AB、AC所對的正三角形的邊長分別是:

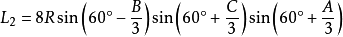

定理七:任意一邊相鄰的兩個劣角的相鄰三等分線的交點,及與這邊相鄰的優角與外角的相鄰三等分線的交點構成正三角形,且點A、B、C所對的正三角形的邊長分別是:
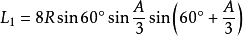
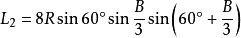
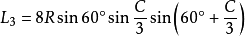
類型
蝸牛三等分角線(有些文獻直接稱此曲線為三等分角線)
馬克勞林三等分角線
等邊三葉(Equilateraltrefoil)
契爾恩豪森三次曲線
丟勒的大青葉(Durer'sfolium)
三次拋物線(Cubicparabola)
偏心率為2的雙曲線
三葉的玫瑰線
拋物線
馬克勞林三等分角線
等邊三葉(Equilateraltrefoil)
契爾恩豪森三次曲線
丟勒的大青葉(Durer'sfolium)
三次拋物線(Cubicparabola)
偏心率為2的雙曲線
三葉的玫瑰線
拋物線

