基本介紹
函式由來,表示方法,解析式,基本性質,函式性質,圖像性質,位置關係,學習方法,知識要點,誤區提醒,和方程的異同,和不等式關係,函式套用,概括整合,常用公式,生活中的套用,常見題型,其它相關,函式和方程,函式和不等式,與二元一次方程的關係,方法小結,區別,
函式由來
“函式”一詞最初是由德國的數學家萊布尼茨在17世紀首先採用的,當時萊布尼茨用“函式”這一詞來表示變數x的冪,即x2,x3,….接下來萊布尼茨又將“函式”這一詞用來表示曲線上的橫坐標、縱坐標、切線的長度、垂線的長度等等所有與曲線上的點有關的變數,就這樣“函式”這詞逐漸盛行。
在中國,古時候的人將“函”字與“含”字通用,都有著“包含”的意思,清代數學家、天文學家、翻譯家和教育家,近代科學的先驅者李善蘭給出的定義是:“凡式中含天,為天之函式。”中國的古代人還用“天、地、人、物”4個字來表示4個不同的未知數或變數,顯然,在李善蘭的這個定義中的含義就是“凡是公式中含有變數x,則該式子叫做x的函式。”這樣,在中國“函式”是指公式里含有變數的意思。
瑞士數學家雅克·柏努意給出了和萊布尼茨相同的函式定義。1718年,雅克·柏努意的弟弟約翰·柏努意給出了函式了如下的函式定義:由任一變數和常數的任意形式所構成的量叫做這一變數的函式.換句話說,由x和常量所構成的任一式子都可稱之為關於x的函式。
1775年,歐拉把函式定義為:“如果某些變數:以某一種方式依賴於另一些變數.即當後面這些變數變化時,前面這些變數也隨著變化,我們把前面的變數稱為後面變數的函式。”由此可以看到,由萊布尼茲到歐拉所引入的函式概念,都還是和解析表達式、曲線表達式等概念糾纏在一起。
首屈一指的法國數學家柯西引入了新的函式定義:“在某些變數間存在著一定的關係,當一經給定其中某一變數的值,其它變數的值也可隨之而確定時,則將最初的變數稱之為‘自變數’,其它各變數則稱為“函式”。在柯西的定義中,首先出現了“自變數”一詞。
1834年,俄國數學家羅巴契夫斯基進一步提出函式的定義:“x的函式是這樣的一個數,它對於每一個x都有確定的值,並且隨著x一起變化。函式值可以由解析式給出,也可以由一個條件給出,這個條件提供了一種尋求全部對應值的方法.函式的這種依賴關係可以存在,但仍然是未知的”.這個定義指出了對應關係。即條件的必要性,利用這個關係以求出每一個x的對應值。
1837年德國數學家狄里克雷認為怎樣去建立x與y之間的對應關係是無關緊要的,所以他的定義是:“如果對於x的每一個值,y總有一個完全確定的值與之對應,則y是x的函式。”
德國數學家黎曼引入了函式的新定義:“對於x的每一個值,y總有完全確定了的值與之對應,而不拘建立x,y之間的對應方法如何,均將y稱為x的函式。”
上面函式概念的演變,我們可以知道,函式的定義必須抓住函式的本質屬性,變數y稱為x的函式,只須有一個法則存在,使得這個函式取值範圍中的每一個值,有一個確定的y值和它對應就行了,不管這個法則是公式或圖象或表格或其他形式。
由此,就有了我們課本上的函式的定義:一般地,在一個變化過程中,如果有兩個變數x與y,並且對於x的每一個確定的值,y都有惟一確定的值與其對應,那么我們就說x是自變數,y是x的函式。
表示方法
 一次函式表示方法
一次函式表示方法一次函式有三種表示方法,如下:
1、解析式法
用含自變數x的式子表示函式的方法叫做解析式法。
2、列表法
把一系列x的值對應的函式值y列成一個表來表示的函式關係的方法叫做列表法。
3、圖像法
用圖象來表示函式關係的方法叫做圖象法。
解析式
一次函式的解析式為:

基本性質
函式性質
1、y的變化值與對應的x的變化值成正比例,比值為k。
即:y=kx+b(k≠0)(k不等於0,且k,b為常數)。
2、當x=0時,b為函式在y軸上的交點,坐標為(0,b)。
當y=0時,該函式圖象在x軸上的交點坐標為(-b/k,0)。
3、k為一次函式y=kx+b的斜率,k=tanθ(角θ為一次函式圖象與x軸正方向夾角,θ≠90°)。
4、當b=0時(即y=kx),一次函式圖象變為正比例函式,正比例函式是特殊的一次函式。
5、函式圖象性質:當k相同,且b不相等,圖像平行;
當k不同,且b相等,圖象相交於Y軸;
當k互為負倒數時,兩直線垂直。
6、平移時:上加下減在末尾,左加右減在中間。
 性質
性質圖像性質
1、作法與圖形:通過如下3個步驟:
(1)列表:每確定自變數x的一個值,求出因變數y的一個值,並列表;
(2)描點:一般取兩個點,根據“兩點確定一條直線”的道理,即在直角坐標系中,以自變數的值為橫坐標,相應的函式值為縱坐標,描出表格中數值對應的各點。
一般地,y=kx+b(k≠0)的圖象過(0,b)和(-b/k,0)兩點即可畫出。
正比例函式y=kx(k≠0)的圖象是過坐標原點的一條直線,一般取(0,0)和(1,k)兩點畫出。
2、性質:(1)在一次函式上的任意一點P(x,y),都滿足等式:y=kx+b(k≠0)。(2)一次函式與y軸交點的坐標總是(0,b),與x軸總是交於(,0)正比例函式的圖象都是過原點。
3、函式不是數,它是指某一變化過程中兩個變數之間的關係。
4、k,b與函式圖象所在象限:
y=kx時(即b等於0,y與x成正比,此時的圖象是一條經過原點的直線)
當k>0時,直線必通過一、三象限,y隨x的增大而增大;
當k<0時,直線必通過二、四象限,y隨x的增大而減小。
y=kx+b(k,b為常數,k≠0)時:
當k>0,b>0,這時此函式的圖象經過一,二,三象限;
當k>0,b<0,這時此函式的圖象經過一,三,四象限;
當k<0,b>0,這時此函式的圖象經過一,二,四象限;
當k<0,b<0,這時此函式的圖象經過二,三,四象限。
當b>0時,直線必通過一、二象限;
當b<0時,直線必通過三、四象限。
特別地,當b=0時,直線通過原點O(0,0)表示的是正比例函式的圖象。
這時,當k>0時,直線只通過一、三象限,不會通過二、四象限。當k<0時,直線只通過二、四象限,不會通過一、三象限。
5、特殊位置關係
當平面直角坐標系中兩直線平行時,其函式解析式中K值(即一次項係數)相等。
當平面直角坐標系中兩直線垂直時,其函式解析式中K值的乘積為-1。
6、直線y=kx+b的圖象和性質與k、b的關係如下表所示:
k>0,b>0:經過第一、二、三象限
k>0,b<0:經過第一、三、四象限
k>0,b=0:經過第一、三象限(經過原點)
結論:k>0時,圖象從左到右上升,y隨x的增大而增大。
k<0,b>0:經過第一、二、四象限
k<0,b<0:經過第二、三、四象限
k<0,b=0:經過第二、四象限(經過原點)
結論:k<0時,圖象從左到右下降,y隨x的增大而減小。
7、將函式向上平移n格,函式解析式為y=kx+b+n,將函式向下平移n格,函式解析式為y=kx+b-n,將函式向左平移n格,函式解析式為y=k(x+n)+b,將函式向右平移n格,函式解析式為y=k(x-n)+b。
位置關係
當平面直角坐標系中兩直線平行時,其函式解析式中k的值(即一次項係數)相等;
當平面直角坐標系中兩直線垂直時,其一次函式斜率的乘積=-1。
關於平面直角坐標系中兩直線垂直時,其函式解析式中K值互為相反數的證明:
如圖,這2個函式互相垂直,但若直接證明,存在困難,不易理解,如果平移平面直角坐標系,使這2個函式的交點交於原點,就會更簡單。就像這一樣,可以設這2個函式的表達式分別為;
y=ax,y=bx。
在x正半軸上取一點(z,0)(便於計算),做與y軸平行的直線,如圖,可知OC=z,AC=a*z,BC=b*z,由勾股定理可得:
OA=√z^2+(a*z)^2
OB=√z^2+(b*z)^2
又有OA^2+OB^2=AB^2,得
z^2+(az)^2+z^2+(bz)^2=(az-bz)^2(因為b小於0,故為az-bz)化簡得:
z^2+a^2*z^2+z^2+b^2*z^2=a^2*z^2-2ab*z^2+b^2*z^2
2z^2=-2ab*z^2
ab=-1
即k=-1
所以兩個K值的乘積為-1。
注意:與y軸平行的直線沒有函式解析式,與x軸平行的直線的解析式為常函式,故上述性質中這兩種直線除外。
 兩一次函式平行
兩一次函式平行 兩一次函式垂直
兩一次函式垂直學習方法
知識要點
1、要理解函式的意義。
2、聯繫實際對函式圖象的理解。
3、隨圖象理解數字的變化而變化。
誤區提醒
1、對一次函式概念理解有誤,漏掉一次項係數不為0這一限制條件;
2、對一次函式圖象和性質存在思維誤區;
3、忽略一次函式自變數取值範圍;(有時x∈Z,其圖象表現為非連續性的點的集合)
4.對於一次函式中,把自變數認為不能等於零。
和方程的異同
1、一次函式和一元一次方程有相似的表達形式。
2、一次函式表示的是一對(x,y)之間的關係,它有無數對解;一元一次方程表示的是未知數x的值,最多只有1個值。
3、一次函式與x軸交點的橫坐標就是相應的一元一次方程的根。
和不等式關係
從函式的角度看,解不等式的方法就是尋求使一次函式y=kx+b的值大於(或小於)0的自變數x的取值範圍的一個過程;
從函式圖象的角度看,就是確定直線y=kx+b在x軸上(或下)方部分所有的點的橫坐標所構成的集合。
對應一次函式y=kx+b,它與x軸交點為(-b/k,0)。
當k>0時,不等式kx+b>0的解為:x>-b/k,不等式kx+b<0的解為:x<-b/k;
當k<0的解為:不等式kx+b>0的解為:x<-b/k,不等式kx+b<0的解為:x>-b/k。
函式套用
概括整合
(2)理清題意是採用分段函式解決問題的關鍵。
常用公式
1、求函式圖象的k值:(y1-y2)/(x1-x2),即k=tanα(α為直線與x軸正方向的夾角)
3、求與y軸平行線段的中點:(y1+y2)/2
4、求任意線段的長:√[(x1-x2)2+(y1-y2)2]
5、求兩個一次函式式圖像交點坐標:解兩函式式
兩個一次函式y1=k1x+b1,y2=k2x+b2,令y1=y2,得k1x+b1=k2x+b2。將解得的x=x0值代回y1=k1x+b1,y2=k2x+b2兩式的任一式,得到y=y0,則(x0,y0)即為y1=k1x+b1與y2=k2x+b2之交點坐標。
6、求任意2點所連線段的中點坐標:((x1+x2)/2,(y1+y2)/2)
7、求任意2點的連線的一次函式解析式:(x-x1)/(x1-x2)=(y-y1)/(y1-y2)(若分母為0,則分子為0)
(x,y)的正負性為+,+(正,正)時該點在第一象限
(x,y)的正負性為-,+(負,正)時該點在第二象限
(x,y)的正負性為-,-(負,負)時該點在第三象限
(x,y)的正負性為+,-(正,負)時該點在第四象限
8、若兩條直線y1=k1x+b1,y2=k2x+b2互相平行,則k1=k2,b1≠b2
9、如兩條直線y1=k1x+b1,y2=k2x+b2互相垂直,則k1×k2=-1
10、設原直線為y=f(x)=kx+b
y=f(x-n)=k(x-n)+b就是直線向右平移n個單位
y=f(x+n)=k(x+n)+b就是直線向左平移n個單位
y=f(x)+n=kx+b+n就是向上平移n個單位
y=f(x)-n=kx+b-n就是向下平移n個單位
口訣:左加右減相對於X,上加下減相對於b。
11、直線y=kx+b與x軸的交點:(-b/k,0),與y軸的交點:(0,b)
生活中的套用
1、當時間t一定,距離s是速度v的一次函式。s=vt。
2、如果水池抽水速度f一定,水池裡水量g是抽水時間t的一次函式。設水池中原有水量S。g=S-ft。
3、當彈簧原長度b(未掛重物時的長度)一定時,彈簧掛重物後的長度y是重物重量x的一次函式,即y=kx+b(k為任意正數)。
常見題型
常見題型一次函式及其圖象是國中代數的重要內容,也是高中解析幾何的基石,更是中考的重點考查內容。
其中求一次函式解析式就是一類常見題型。現以部分中考題為例介紹幾種求一次函式解析式的常見題型。希望對大家的學習有所幫助。
一、定義型
例1、已知函式是一次函式,求其解析式。
解:由一次函式定已知

注意:利用定義求一次函式y=kx+b解析式時,要保證k≠0。如本例中應保證m-3≠0。
二、點斜型
例2、已知一次函式y=kx-3的圖象過點(2,-1),求這個函式的解析式。
解:一次函式的圖象過點(2,-1),,即k=1。故這個一次函式的解析式為y=x-3。
變式問法:已知一次函式y=kx-3,當x=2時,y=-1時,求這個函式的解析式。
三、兩點型
例3、已知某個一次函式的圖象與x軸、y軸的交點坐標分別是(-2,0)、(0,4),則這個函式的解析式為_____。
解:設一次函式解析式為y=kx+b
由題意得,

故這個一次函式的解析式為y=2x+4。
四、圖像型 圖1
圖1
 圖1
圖1例4、已知某個一次函式的圖象如圖1所示,則該函式的解析式為__________。
解:設一次函式解析式為y=kx+b由圖可知一次函式的圖象過點(1,0)、(0,2)有

所以k=-2
b=2
故這個一次函式的解析式為y=-2x+2。
五.斜截型
例5、已知直線y=kx+b與直線y=-2x平行,且在y軸上的截距為2,則直線的解析式為___________。
解析:兩條直線;。當k1=k2,b1≠b2時,


六.平移型
例6、把直線y=2x+1向下平移2個單位得到的圖象解析式為___________。
解析:設函式解析式為y=kx+b,直線y=2x+1向下平移2個單位得到的直線y=kx+b與直線y=2x+1平行

直線y=kx+b在y軸上的截距為b=1-2=-1。
七、實際套用型
例7、某油箱中存油20升,油從管道中勻速流出,流速為0.2升/分鐘,則油箱中剩油量Q(升)與流出時間t(分鐘)的函式關係式為___________。
解:由題意得Q=20-0.2t,即Q=-0.2t+20

故所求函式的解析式為Q=-0.2t+20()
注意:求實際套用型問題的函式關係式要寫出自變數的取值範圍,別忘了考慮變數存在等於0的情況。
八、面積型
例8、已知直線y=kx-4與兩坐標軸所圍成的三角形面積等於4,則直線解析式為__________。
解:易求得直線與x軸交點為,所以


故直線解析式為y=2x-4或y=-2x-4。
九、對稱型
若直線與直線y=kx+b關於
(1)x軸對稱,則直線的解析式為y=-kx-b;
(2)y軸對稱,則直線的解析式為y=-kx+b;
(3)直線y=x對稱,則直線的解析式為;
(4)直線y=-x對稱,則直線的解析式為;
(5)原點對稱,則直線的解析式為y=kx-b。
例9、若直線l與直線y=2x-1關於y軸對稱,則直線l的解析式為____________。
解:由(2)得直線l的解析式為y=-2x-1。
十、開放型
例10、已知函式的圖象過點A(1,4),B(2,2)兩點,請寫出滿足上述條件的兩個不同的函式解析式,並簡要說明解答過程。
解:
(1)若經過A、B兩點的函式圖象是直線,由兩點式易得y=-2x+6
(2)由於A、B兩點的橫、縱坐標的積都等於4,所以經過A、B兩點的函式圖象還可以是雙曲線。
十一、幾何型
例11、如圖2,在平面直角坐標系中,A、B是x軸上的兩點,以AO、BO為直徑的半圓分別交AC、BC於E、F兩點,若C點的坐標為(0,3)。(1)求圖象過A、B、C三點的二次函式的解析式,並求其對稱軸;(2)求圖象過點E、F的一次函式的解析式。
解:(1)由直角三角形的知識易得點A(-3√3,0)、B(√3,0),由待定係數法可求得二次函式解析式為,對稱軸是x=-√3 (2)連結OE、OF,則、。過E、F分別作x、y軸的垂線,垂足為M、N、P、G,易求得E、F,由待定係數法可求得一次函式解析式。
 圖2
圖2十二、方程型
例12、若方程x2+3x+1=0的兩根分別為,求經過點P和Q的一次函式圖象的解析式
解:由根與係數的關係得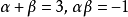
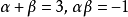



設過點P、Q的一次函式的解析式為y=kx+b
則有

解得

其它相關
函式和方程
1、從形式上看:一次函式y=kx+b,一元一次方程ax+b=0。
2、從內容上看:一次函式表示的是一對(x,y)之間的關係,它有無數對值;一元一次方程表示的是未知數x的值,最多只有1個值。
3、相互關係:一次函式與x軸交點的橫坐標就是相應的一元一次方程的根。例如:y=4x+8與x軸的交點是(-2,0)、則一元一次方程4x+8=0的根是x=-2。
函式和不等式
解不等式的方法:從函式的角度看,就是尋求使一次函式y=kx+b的值大於(或小於)0的自變數x的取值範圍;
從函式圖象的角度看,就是確定直線y=kx+b在x軸上(或下)方部分所有的點的橫坐標所構成的集合。
對應一次函式y=kx+b,它與x軸交點為(-b/k,0)。
當k>0時,不等式kx+b>0的解為:x>-b/k,不等式kx+b<0的解為:x<-b/k;
當k<0的解為:不等式kx+b>0的解為:x<-b/k,不等式kx+b<0的解為:x>-b/k。
與二元一次方程的關係
1、以二元一次方程組ax+by=c的解為坐標的點組成的圖象與一次函式y=(-a/b)x+c/b的圖象相同。
2、二元一次方程組a1x+b1y=c1,a2x+b2y=c2的解可以看作是兩個一次函式y=(-a1/b1)x+c1/d1和y=(-a2/b2)x+c2/d2的圖象的交點。
方法小結
把方程組中的兩個二元一次方程改寫成一次函式的形式,然後作出它們的圖象,找出兩圖像的交點,即可知方程組的解。
區別
二元一次方程有兩個未知數,而一次函式只是說未知數的次數為一次,並未限定幾個變數,因此二元一次方程只是一次函式中的一種。
1、面直角坐標系中分別描繪出以二元一次方程的解為坐標的點,這些點都在相應的一次函式的圖象上。如方程2x+y=5有無數組值,像x=1,y=3;x=2,y=1;…以這些解為坐標的點(1,3),(2,1)…都在一次函式y=-2x+5的圖象上。
2、一次函式圖象上任取一點,它的坐標都適合相應的二元一次方程。如在一次函式y=-x+2的圖象上任取一點(3,-1),則x=3,y=-1一定是二元一次方程x+y=2的一組解。

