作者簡介 劉徽 (生於公元250年左右),是中國
數學史 上一個非常偉大的數學家,在世界數學史上,也占有傑出的地位.他的傑作《
九章算術注 》和《海島算經》,是我國最寶貴的數學遺產。
《
九章算術 》約成書於東漢之初,共有246個問題的解法.在許多方面:如解
聯立方程 ,分數
四則運算 ,正負數運算,幾何圖形的體積面積計算等,都屬於世界先進之列,但因解法比較原始,缺乏必要的證明,而
劉徽 則對此均作了補充證明.在這些證明中,顯示了他在多方面的創造性的貢獻.他是世界上最早提出
十進小數 概念的人,並用十進小數來表示無理數的
立方根 .在代數方面,他正確地提出了正負數的概念及其加減運算的法則;改進了
線性方程組 的解法.在幾何方面,提出了“
割圓術 ”,即將圓周用內接或
外切 正多邊形 窮竭的一種求
圓面積 和圓周長的方法.他利用割圓術科學地求出了圓周率π=3.14的結果.劉徽在割圓術中提出的“
割之彌細,所失彌少,割之又割以至於不可割,則與圓合體而無所失矣 ”,這可視為中國古代極限觀念的佳作。
劉徽
簡介 《海島算經》由
劉徽 於三國魏景元四年(公元263年)所撰,本為《
九章算術注 》之第十卷,題為《
重差 》。唐初開始單行,體例亦是以套用問題集的形式。研究的對象全是有關高與距離的測量,所使用的工具也都是利用
垂直關係 所連線起來的測竿與橫棒。有人說是實用三角法的啟蒙,不過其內容並未涉及
三角學 中的正
餘弦 概念。所有問題都是利用兩次或多次測望所得的數據,來推算可望而不可及的目標的高、深、廣、遠。此卷書被收集於
明成祖 時編修的
永樂大典 中,現保存在英國劍橋大學圖書館。
劉徽 也曾對九章算數重編並加以注釋。全書共9題,全是利用測量來計算高深廣遠的問題,首題測算海島的高、遠,故得名。
內容 《海島算經》共九問。都是用
表尺 重複從不同位置測望,取測量所得的差數,進行計算從而求得山高或谷深,這就是
劉徽 的重差理論。《海島算經》中,從題目文字可知所有計算都是用
籌算 進行的。“為實”指作為一個分數的分子,“為法”指作為分數的
分母 。所用的
長度單位 有里、丈、步、尺、寸;1里=180丈=1800尺;1丈=10尺:1步=6尺,1尺=10寸。
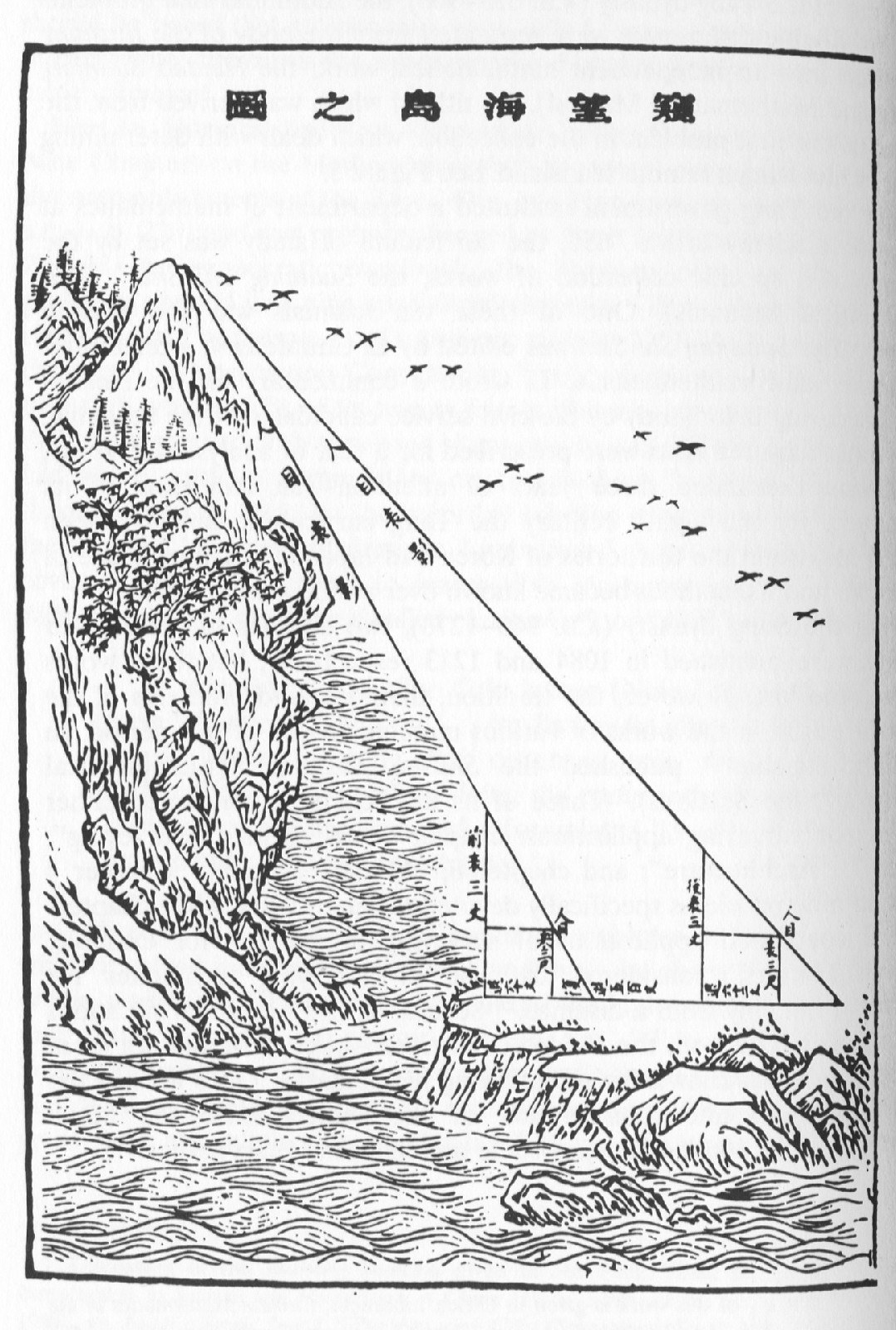
望海島圖
(1) 今有望海島,立兩表,齊高三丈,前後相去千步,令後表與前表參相直。從前表卻行一百二十三步,人目著地取望島峰,與表末參合。從後表卻行一百二十七步,人目著地取望島峰,亦與表末參合。問島高及去表各幾何?答曰:島高四里五十五步;去表一百二里一百五十步。
翻譯:假設測量海島,立兩根表高均為3丈,前後相距1000步,令後表與前表在同一直線上,從前表退行123 步,
人目著地觀測到
島峰 ,從後表退行127步,人目著地觀測到島峰,問島高多少 島與前表相距多遠?
術曰:以表高乘表間為實;相多為法,除之。所得加表高,即得島高。求前表去島遠近者:以前表卻行乘表間為實;相多為法。除之,得島去表數。
(2) 今有望松生山上,不知高下。立兩表齊,高二丈,前後相去五十步,令後表與前表參相直。從前表卻行七步四尺,薄地遙望松末,與表端參合。又望松本,入表二尺八寸。復從後表卻行八步五尺,薄地遙望松末,亦與表端參合。問松高及山去表各幾何?答曰:松高一十二丈二尺八寸;山去表一里二十八步、七分步之四。
術曰:以入表乘表間為實。相多為法,除之。加入表,即得松高。求表去山遠近者:置表間,以前表卻行乘之為實。相多為法,除之,得山去表。
(3) 今有南望方邑,不知大小。立兩表東、西去六丈,齊人目,以索連之。令東表與邑 東南隅及東北隅參相直。當東表之北卻行五步,遙望邑西北隅,入索東端二丈二尺六寸半。又卻北行去表一十三步二尺,遙望邑西北隅,適與西表相參合。問邑方及邑去表各幾何?答曰:邑方三里四十三步、四分步之三;邑去表四里四十五步。
術曰:以入索乘後去表,以兩表相去除之,所得為景長;以前去表減之,不盡以為法。置後去表,以前去表減之,余以乘入索為實。實如法而一,得邑方。求去表遠近者:置後去表,以景長減之,余以乘前去表為實。實如法而一,得邑去表。
(4) 今有望深谷,偃矩岸上,令勾高六尺。從勺端望谷底,入下股九尺一寸。又設重矩於上,其矩間相去三丈。更從勺端望谷底,入上股八尺五寸。問谷深幾何?答曰:四十一丈九尺。
術曰:置矩間,以上股乘之,為實。上、下股相減,余為法,除之。所得以勾高減之,即得谷深。
(5) 今有登山望樓,樓在平地。偃矩山上,令勾高六尺。從勾端斜望樓足,入下股一丈二尺。又設重矩於上,令其間相去三丈。更從勾端斜望樓足,入上股一丈一尺四寸。又立小表於入股之會,復從勾端斜望樓岑端,入小表八寸。問
樓高 幾何?答曰:八丈。
術曰:上、下股相減,余為法;置矩間,以下股乘之,如勾高而一。所得,以入小表乘之,為實。實如法而,即是樓高。
(6) 今有東南望波口,立兩表南、北相去九丈,以索薄地連之。當北表之西卻行去表六丈,薄地遙望波口南岸,入索北端四丈二寸。以望北岸,入前所望表里一丈二尺。又卻行,後去表一十三丈五尺。薄地遙望波口南岸,與南表參合。問波口廣幾何?答曰:一里二
百步 。
術曰:以後去表乘入索,如表相去而一。所得,以前去表減之,余以為法;復以前去表減後去表,余以乘入所望表里為實,實如法而一,得波口廣。
(7) 今有望清淵下有白石。偃矩岸上,令勾高三尺。斜望水岸,入下股四尺五寸。望白石,入下股二尺四寸。又設重矩於上,其間相去四尺。更從勾端斜望水岸,入上股四尺。以望白石,入上股二尺二寸。問水深幾何?答曰:一丈二尺。
術曰:置望水上、下股
相減 ,余以乘望石上股為上率。又以望石上、下股相減,余以乘望水上股為下率。兩率相減,余以乘矩間為實;以二差相乘為法。實如法而一,得水深。
(8) 今有登山望津,津在山南。偃矩山上,令勾高一丈二尺。從勾端斜望津南岸,入下股二丈三尺一寸。又望津北岸,入前望股里一丈八寸。更登高岩,北卻行二十二步,上登五十一步,偃矩山上。更從勾端斜望津南岸,入上股二丈二尺。問津廣幾何?答曰:二里一百二步。
術曰:以勾高乘下股,如上股而一。所得以勾高減之,余為法;置北行,以勾高乘之,如上股而一。所得以減上登,余以乘入股里為實。實如法而一,即得津廣。
(9) 今有登山臨邑,邑在山南。偃矩山上,令勾高三尺五寸。令勾端與邑東南隅及東北隅參相直。從勾端遙望東北隅,入下股一丈二尺。又施橫勾於入股之會,從立勾端望西北隅,入橫勾五尺。望東南隅,入下股一丈八尺。又設重矩於上,令矩間相去四丈。更從立勾端望東南隅,入上股一丈七尺五寸。問邑廣長各幾何?答曰:南北長一里百步;東西廣一里三十三步、少半步。
術曰:以勾高乘東南隅入下股,如上股而一,所得減勾高,余為法;以東北隅下股減東南隅下股,余以乘矩間為實。實如法而一,得邑南北長也。求邑廣:以入橫勾乘矩間為實。實如法而一,即得邑東西廣。
歷代研究 南北朝數學家
祖沖之 曾為《九章重差圖》作注。唐朝將《九章重差圖》從《劉徽九章算術注》中分離出來單獨
成書 ,以第一題“今有望海島”取名為《海島算經》。
唐高宗 顯慶元年(656年)數學家李淳風等注釋《
算經十書 》,作為國子監學習和考試用書,《海島算經》就是《算經十書》之一,並且規定《海島算經》的學習期限為三年,是其他算經學習期限的三倍,可見《海島算經》在唐代受重視的程度。
北宋 元豐七年(1084年)和
南宋寧宗 嘉定六年(1213年)先後刻印兩次。但
宋刻本 《海島算經》後來遺失。
南宋 秦九韶 研究過類似於海島算經的測量書題目《表望浮屠》南宋數學家
楊輝 《
續古摘奇算法 》討論了四種
測量問題 ,包括來自《海島算經》海島題,並指出“登高望松,遙望波口,非三望之術乎?清淵白石、登山
臨邑 ,非四望之術乎?”。明
永樂 年間收入《永樂大典》,但只存
劉徽 文字和
李淳風 注,劉徽原圖和劉徽所作的注釋已不存。
元朝 數學家
朱世傑 《
四元玉鑒 》《勾股測望》門第四,六,七,八等四問用
天元術 闡述《海島算經》的《望海島》,《望深谷》,《南望方邑》,《望清淵》。清
乾隆 時代,經學家
戴震 將《海島算經》文字,從《
永樂大典 》中輯錄出來收入《
四庫全書 》。 清代數學家李潢著《
海島算經細草圖說 》,沈欽裴著《
重差圖說 》,均以歐幾里德幾何學論證,已失劉徽原意。 李鏐著《海島算經緯筆》。到民國時期,中算史家
李儼 《重差術流源及其新注》和《中國古代中算家的測繪術》,《海島算經新注》都對《海島算經》有所論述。
秦九韶《表望浮屠》繼承《海島算經》
中國數學家
白尚恕 對海島算經有較詳細的論證。
吳文俊 院士論文《我國古代測望之學重差理論評介兼評數學史研究中的某些方法問題》 與《海島算經古證探源》兩篇論文對《海島算經》有詳細的論證,前文批評一些前人對《海島算經》的論證中添加
歐幾里德幾何 的
平行線 或利用
相似形 理論或後代的代數論證的方法,顛倒歷史,都是錯誤的方法,並提出正確的論證,必須以
劉徽 時代的
出入相補原理 為基礎,才能還原《海島算經》的本來面目。
傳播海外 《海島算經》在唐代傳入朝鮮、日本。最早向西方介紹《海島算經》的是19世紀來華傳教士
偉烈亞力 。他1852年在《
北華捷報 》(North China Herald,《
字林西報 》前身)發表的論文:《中國數學科學札記》(Jottings on the Sciences of Chinese Mathematics)。偉烈亞力在文中介紹了《海島算經》,說此書是“一部關於實用三角學的九個問題”。1913年
日本數學 史家
三上義夫 在其英文著作《中國與日本數學的發展》第五章《海島算經》 中譯出頭三則問題1932年法國數學家 L·van·Hee 翻譯《海島算經》全文
1986年澳大利亞華人數學家洪天賜和美國數學家弗蘭克·斯委特茲將《海島算經》全文翻譯成英文還有日文翻譯本和
俄文 翻譯本。
《海島算經》的英文翻譯本
評價 3世紀
劉徽 《海島算經》運用二次、三次、四次
測望法 ,是
測量學 歷史上領先的創造中外學者對《海島算經》的成就,給予很高的評價。《海島算經》的英譯者和研究者,美國數學家弗蘭克·斯委特茲,在比較
西歐 測量學從
古代希臘 、
羅馬 直到
文藝復興 時期的發展,認為希臘測量術,重點在測量器具的運用,而其數學水準遠不如劉徽《海島算經》,直到文藝復興時代,才差強達到《海島算經》水準。他還指出17世紀初
義大利 來華傳教士利瑪竇和中國徐光啟合著的《
測量法義 》十五題,並未能達到或超越《海島算經》。他結論;“簡而言之,在測量數學領域,中國人的成就,超越
西方世界 約一千年。”
《中國數學大系》一書中評價《海島算經》:“使中國測量學達到登峰造極的地步。在西歐直到16,17世紀,才出現二次測量術的記載,到18世紀,才有了三、四次測量之術,可見中國古代測量學的意境之深,功用之廣”。
劉徽 《海島算經》的測量術,實比歐洲早一千三百至一千五百年。