基本介紹
內容簡介
出版背景
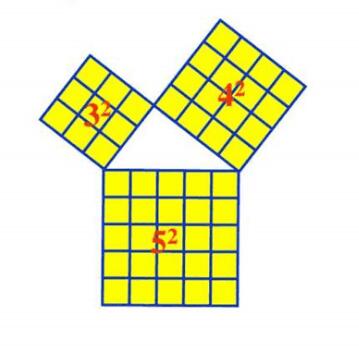
勾股定理


《〈九章算術〉與〈周髀算經〉》是劉金貴創作的中國畫。2016年11月22日 - 12月11日,該作品在中國文學藝術界聯合會、中華人民共和國財政部、中華人民共和國文化部主辦的“中華史詩美術大展”中展出,展出地址為中國國家博物館。
《孫子算經》是中國古代重要的數學著作,成書大約在四、五世紀,也就是大約一千五百年前,作者生平和編寫年不詳。傳本的《孫子算經》共三卷。卷上敘述算籌記數的縱橫相間制度和籌算乘除法,卷中舉例說明籌算分數算法和籌算開平方法。...
(一)《周髀算經》簡介 在中國古代算書中,《周髀算經》、《九章算術》、《孫子算經》、《五曹算經》、《夏侯陽算經》、《孫丘建算經》、《海島算經》、《五經算術》、《綴術》、《緝古算機》等10部算書,被稱為“算經十...
《九章算術》(省稱《九章》)是中國最重要的數學經典,它之於中國和東方數學,大體相當於《幾何原本》之於希臘和歐洲數學。在世界古代數學史上,《九章》與《原本》像兩顆璀燦的明珠,東西輝映。《九章》之前還有一部《周髀算經》,它...
這期間他對《九章算術》《周髀算經》《七曜曆書》等十幾部涉及日月運行、山川地理的著作悉心研究,著出了《稽極》《曆書》和《五經述議》,這些都成為當時的天文名著。當讀到這些觀點新穎、見解獨到的著作時,不計其數的儒者和年輕...
內算、綴術與外算 古曆法與星占(一)古曆法與星占(二)天人合一 第二 蓋天之論 蓋天論的源流 蓋天儀 天圓地方 第三 陰陽之氣 璇璣玉衡 度景量天 《周髀算經》蓋天曆法 二十四節氣 天氣、地氣、人氣 七衡六間圖 陰陽五行...
三《周髀算經》和陳子 四《九章算術》和張蒼、耿壽昌 第二節分數、今有術與盈不足術 一分數及其四則運算法則 二今有術與衰分術、均輸術 三盈不足術 第三節面積、體積、勾股與測望 一面積 二體積 三勾股定理與解勾股形 四勾股...
吳國趙爽注《周髀算經》,漢末魏初徐岳撰《九章算術》注,魏末晉初劉徽撰《九章算術》注、《九章重差圖》都是出現在這個時期。趙爽與劉徽的工作為中國古代數學體系奠定了理論基礎。趙爽是中國古代對數學定理和公式進行證明與推導的最早的...
2.2.1 歐幾里得與《原本》2.2.2 阿基米德的數學成就 2.2.3 阿波羅尼奧斯與圓錐曲線論 2.3 亞歷山大後期和希臘數學的衰落 3 中世紀的中國數學 3.1 《周髀算經》與《九章算術》3.1.1 古代背景 3.1.2 《周髀算經》3.1.3 ...
1、我國最早的數學書籍《周髀算經》(約成書於公元前1世紀),記載圓周率是“徑一周三”,三國時期,數學家劉徽認為“古之九數,圓周率三圓徑率一,其術疏舛。”而把圓周率推算到3.1416,世界領先上千年。可見,現今和漢代對圓形各...
著有匯校《九章算術》(1990)及其增補版(2004)、《中國古代數學》(1991,1994,1995,1997,2004)、《古代世界數學泰斗劉徽》(1992,1995)、《九章算術》譯註(1998)、點校《算經十書》(1998,2001,其中《周髀算經》系與劉鈍...
在古代數學名著《九章算術》(公元1世紀)中,記載了用算籌解一次聯立方程組的一般方法。所採用的“正負術”中給出了負數的概念,建立了正、負數的運算法則。中國古代把開各次方和解二次以上的方程,統稱為“開方”。在《周髀算經》和...
1.1 《周髀算經》與勾股定理 1.2 《九章算術》§2 魏晉、南北朝時期的數學 2.1 劉徽的數學成就 2.2 百雞問題 2.3 祖沖之父子的貢獻 2.4 中國古代的代數 §3 宋元時期的數學 3.1 賈憲三角和增乘開方法 3.2 秦九韶與...
《墨子》卷一〇《經上》郭象注成玄英疏《南華真經註疏》卷八《庚桑楚》《文子》卷上《道原》尸佼撰汪繼培輯《尸子》卷下 陸佃注《鵾冠子》卷上《環流》劉安撰高誘注《淮南子》卷一《原道訓》趙爽注甄鸞重述李淳風釋《周髀算經》卷...
眾所周知,伏羲氏從河圖推演出先天八卦,周文王從洛書推演出後天八卦,漢代的《周髀算經》推演出勾股定理,楊雄在《太玄經》中用河洛理論推演出六十納音,宋代陳摶以河洛理論繪製出《易龍圖》,推演出七曜和二十八宿,朱熹據此推演出...
《史記》卷二記載大禹治水時“左準繩,右規矩”。趙爽注《周髀算經》中有“禹治洪水,……望山川之形,定高下之勢,……乃勾股之所由生也。”意即禹治洪水,要先測量地勢的高低,就必定要用勾股的道理。這也說明矩起源於很遠的...
此外﹐又有北極(北辰)說﹐例如伏勝在《尚書大傳》中寫道:“璇者﹐還也﹐璣者幾也﹐微也﹐其變幾微而行動者大﹐謂之璇璣﹐是故璇璣謂之北極。”《說苑》則說:“璇璣謂北辰﹐勺陳樞星也。”《周髀算經》稱北辰皆曰璇璣﹐而《...
中國古算書《周髀算經》(約公元前2世紀)的中有“徑一而周三”的記載,意即取 。漢朝時,張衡得出 ,即 (約為3.162)。這個值不太準確,但它簡單易理解。公元263年,中國數學家劉徽用“割圓術”計算圓周率,他先從圓內接正...
《黃帝內經》與人體 中醫的經驗科學性質 地圖與地理 秦漢時期的農業 漢代的農業 第五章 析物之理 中國古代科技的創造性思維 取象類比的“詩性”思維 “天人合一”的整體思維 《周易》“象數”之學與科學 《周髀算經》的宇宙模型 ...
(表格信息來源:《漢語大詞典》《現代漢語詞典》《漢語大字典》)古籍釋義 說文解字 【卷四】【目部】香衣切(xī)望也。從目,稀省聲。海岱之閒謂眄曰睎。說文解字注 【卷四】【目部】(睎)望也。《西都賦》曰:“睎秦嶺...
李文林,中國科學院數學與系統科學研究院研究員,曾任中國科學院數學研究所副所長、中國數學會秘書長、國際數學聯盟數學史委員會委員,撰寫《數學史概論》《數學的進化》等學術著作。王元,中國科學院數學與系統科學研究院院士,撰寫《數論在...
