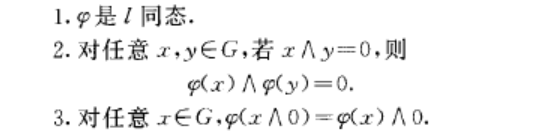
l同態(L-homomorphism)一類特殊的同態. 群與格的同態套用于格群.設G與H是兩個格群。
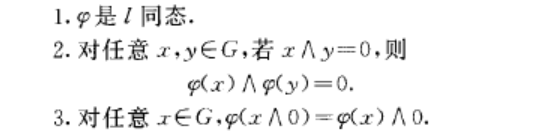
輸入和輸出具有相同運算的同態系統，可以通過 其線性部分L，把所規定運算組合的輸入矢量分離。故亦稱為同態濾波器。在信號處理的套用中，乘法同態系統和卷積同態系統是兩類常見而又重要的服從廣義疊加定理的非線性系統。它們都是輸入和輸出具有相同運算的同態系統。乘法同態系統 乘法同態系統 乘法同態系統的基本原理是：設...
l表示 l表示(L-representation)刻畫格環的重要工具.若G是滿足加法交換的偏序群，E(G)表示G的群自同態環,BE E(G)，定義B,0若且唯若B(G+)G+，則E(G)成為偏序環，稱為G的群自同態偏序環。格環R到某個交換格群G的群自同態偏序環E(G)的L同態(即保持+，·，八，V運算)稱為R的一個L表示.
同態的同餘核 同態的同餘核（congruence kernel of a homo- morphism）是1993年公布的數學名詞。公布時間 1993年經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
同態的理想核 同態的理想核（ideal kernel of a homomorphism）是1993年公布的數學名詞。公布時間 1993年經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
l理想 l理想(L-ideal)亦稱L幻.是一類重要的凸l子群.格群G的正規凸L子群，稱為G的L理想.{0}及G本身是G的L理想，稱為G的平凡L理想.若滬是格群G到格群H的滿L同態 則:
1.存在O單同態:M-＞F;2.當K是f模，gyp: M-＞K是O同態;則存在惟一的L同態尹:F-＞K，使得滬尹一獷，即圖1是可換的，此時稱f模F為M上的自由f模，其中O(單)同態即為保序的(單)模同態，L同態表示既為格同態又為模同態.類似於自由格群.設R是有單位元的左f環，X是集合，F為f模，若:1.存在內射...
投射f模(projective f-module)具有格序結構的投射模.投射f模，具有格序結構的投射模.設P是有單位元的左f環上的左f模。若給定f模M,N，滿L同態}: M->N和L同態}p: P->N，存在L同態尹:P->M，使得尹}=}P，即是可換的，則稱屍為投射f模，其中的滿L同態要求正錐滿足州M+)=N十·對於投射f模有類...
1.F是由Sπ生成的l群；2.若σ是S到任意格序群H的映射，則存在F到H的l同態τ，使π°τ=σ，即圖是可換的；則稱(F，π)為S上的自由格序群，S為F的自由生成元集。任意基數α的集合S上的自由格序群F是存在的，且在同構的意義下是惟一的。若(F，π)是偏序群G上的自由格序群，則：1.若G是交換...
1。若GE('H)是G的L子群，則HE0l.2.若GE(',H是一個格序群，甲是一個L同態，使得抓G)=H，則HE('.)3.若y.是招了中的一類格序群，則I I ' E 0u.由等式xy = yx定義的可換簇記為了;由等式(二八yz-x,z八yz)定義的可表示簇記為J;由等式二一二定義的格序群簇記為丫;由等式二一1定義的只...
其中常數C≥0，l是Γ的連續實值同態，g是Γ上非負連續二次型，μ是X\{0}上的正對稱測度且滿足 並且，C,l,g,μ由ψ惟一決定，即 ，μ是關於ψ的列維測度，上述方程稱為列維-辛欽公式。列維測度 列維測度是在X\{0}上與(μₜ)相關聯的一個正測度。設(μₜ)是X上的卷積半群，則在X\{0}上的正...
在抽象代數中，Ado定理指出每一個有限維的，在一個零特徵的域K上的李代數L都可被看作是一個用交換子李括弧定義的關於方塊矩陣的李代數。更為準確地說，定理指出L在K上有一個在有限維向量空間V上的忠實線性表示，使得L與一個V自同態的子代數同構。簡介 在抽象代數中，Ado定理指出每一個有限維的，在一個零...
在同態、逆同態和與正則語言相交下保持封閉的語言族稱為滿三重組。對並運算封閉的滿三重組稱為滿半AFL。對乘冪閉包封閉的滿半 AFL稱為滿AFL。從一個語言族出發，經上述代數運算後得到的閉包分別稱為由生成的滿三重組、滿半AFL和滿AFL,以（）、()和（）表之。如果語言族只包含一個語言L，則由生成的結構分別...
在三維多面體的情況下，透鏡空間可以通過將兩個實心圓弧通過其邊界的同態粘合在一起而被可視化。 通常，如上所述，三球（3-sphere）以及S×S因為它們是三維的，所以兩者都可以被計算。三維透鏡空間L（p，q）由Tietze在1908年引入。它們是第三種已知的三維多面體實例，它們不是由它們的同源組和基本組決定的 ，以...
單純鏈映射(simplicial chain map)是由單純映射決定的鏈映射。鏈映射是聯繫復形的鏈群之間的一種系列同態。為了使復形的鏈群之間的同態能誘導出同調群之間的同態，因而它應將閉鏈與邊緣鏈分別映成閉鏈與邊緣鏈。概念 單純鏈映射(simplicial chain map)是由單純映射決定的鏈映射。設f：K→L是一個單純映射，定義...
同態 給了兩個多面體|K|、|L|之間的一個連續映射F：│K│→│L│，可以將K適當重分成另一復形K┡,並用一個單純映射去逼近F。利用這個單純映射導出的同調群之間的同態得到Hn(│K┡│；G)到Hn(│L│；G)的同態，並且可以證明，Hn(│K┡│；G)與Hn(|K|;G)自然地同構。 於是記此同態為Fn：Hn(|K|...
設V是辛空間，ψ是V上的線性變換，且g(ψ(x)，ψ(y))=g(x，y)對任意的x，y∈V成立，則稱ψ是V上的辛變換。定義介紹 定義一 設L為數域F上的一個n=2m維辛空間，σ為線性空間L的一個自同態，如果對於任何 ，恆有 則σ叫做一個辛變換。定義二 辛變換是辛空間的等度量變換，設V為辛空間，對 ...
例如，一個群模去其換位子群的商群(稱為交換化)得到一個交換群，從而交換化成為群範疇到交換群範疇的一個變換，且這個變換保持著群同態及其合成。事實上，這就是函子的思想。在域F上的線性空間範疇中，任一線性空間L必有惟一的對偶空間L=Hom(L，F)，“*”可看成這個線性空間範疇到自身的一個變換。儘管當L...
同調群所具有的一種性質。復形偶(K，L)與K和L的各種同調關係表現為它們的同調群組成的一個正合的序列，即單純同調序列，它在單純同調論中有很多套用。設(K，L)是復形偶，其中K是n維復形，定義三種同態(為方便省去下標q)：1.包含映射i：|L|→|K|誘導出同態 2.包含映射j：(|K|，)→(|K|，|L|)誘...
根類(radical class)全體根環做成的環類一般根論中的重要環類，常和對應的根性質用同一個符號表示.給定結合環類的一個子類男，稱屬於此子類中的環為，男環，就得到一個性質男.子類l成為根類的充分必要條件是:男環的同態像仍是男環;若一個環A，它的任意非零同態像都含有非零男理想，則A本身是男環.上述...
王爽，男，博士學位，現任杭州鍩崴信息科技有限公司董事長，四川大學華西醫院特聘教授，同濟大學附屬醫院客座教授。2018年中組部引進“海外青年高層次人才”。曾任美國加州大學聖地亞哥分校（UCSD）醫學院生物醫學信息系教授。國際同態加密協會創始委員。人物簡介 王爽博士現任鍩崴科技創始人、董事長，同濟大學附屬醫院客座...
