如果系統的輸入和輸出解釋為矢量空間中的矢量,運算規則□和〇對應於矢量加法,則系統變換H〔·〕就是代數上從輸入矢量空間到輸出矢量空間的一種線性變換,稱為同態變換。
基本介紹
- 中文名:同態變換
- 外文名:homomorphic transform
- 套用學科:通信
定義
 圖1
圖1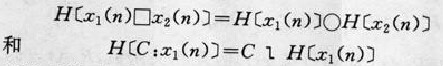 圖2
圖2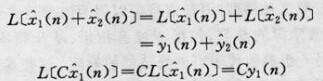 圖3
圖3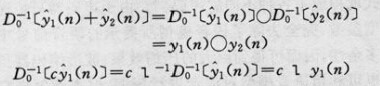 圖4
圖4乘法同態系統
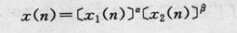 圖5
圖5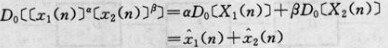 圖6
圖6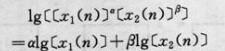 圖7
圖7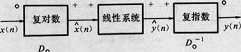
如果系統的輸入和輸出解釋為矢量空間中的矢量,運算規則□和〇對應於矢量加法,則系統變換H〔·〕就是代數上從輸入矢量空間到輸出矢量空間的一種線性變換,稱為同態變換。
 圖1
圖1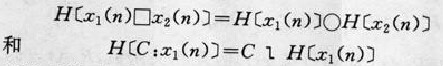 圖2
圖2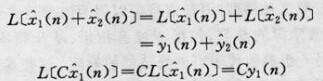 圖3
圖3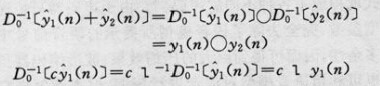 圖4
圖4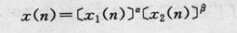 圖5
圖5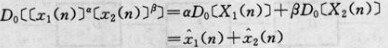 圖6
圖6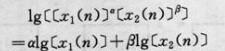 圖7
圖7
如果系統的輸入和輸出解釋為矢量空間中的矢量,運算規則□和〇對應於矢量加法,則系統變換H〔·〕就是代數上從輸入矢量空間到輸出矢量空間的一種線性變換,稱為同態...
乘法同態系統(multiplicative homomorphic system)輸入信號組合和輸出信號組合均為運算乘,取冪,並服從廣義疊加定理的系統。...
線性映射( linear mapping)是從一個向量空間V到另一個向量空間W的映射且保持加法運算和數量乘法運算,而線性變換(linear transformation)是線性空間V到其自身的線性...
射影變換群(projective transformation group),簡稱射影群。是一類基本的變換群,即由射影空間中全體射影變換所構成的變換群。變換群是幾何學研究的重要對象。即由...
默比烏斯變換(Mobius transformation),也稱莫比烏斯變換,是數論中的一種重要變換。默比烏斯變換是以數學家奧古斯特·費迪南德·莫比烏斯命名的, 它也被叫做homographic ...
同態系統(homomorphic system) 通過非線性變換將非線性組合信號變換為線性組合,便於進行線性處理的一類系統的總稱。...
半線性變換(semilinear transformation)是線性變換的推廣。設V與V′分別是域P與P′上的線性空間,ρ為P與P′的同構,若V與V′的映射φ滿足條件:1.對任意α,β...
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。仿射變換群是指仿射空間A的所有自同構組成A的置換群的子群,稱為A的...
《信號處理中的數學變換和估計方法》是2004年清華大學出版社出版的圖書,作者是徐伯勛。...
冪零變換是代數學名詞,指一類特殊的線性變換。線性代數的重要概念之一。設σ是數域P上的線性空間V的一個變換。若對於V中的任意向量α,β與P中的任意數k,有σ...
卷積同態系統(homomorphic system for convolution) 輸入信號組合和輸出信號組合均為卷積運算,並且服從廣義疊加定理的同態系統。...
現階段,比較流行的圖像增強技術有:灰度變換、同態濾波、直方圖修正、頻域濾波。其中,灰度變換法、直方圖法屬於空域方法,而同態濾波法、頻域濾波屬於頻域法。在實際生活...
在同調代數中,蛇引理是構造長正合序列的關鍵工具,此引理在任何阿貝爾範疇中皆成立。依此構造的同態通常稱作連結同態。...
例如,在集合論中,態射就是函式;在群論中,它們是群同態;而在拓撲學中,它們是...函子可以視為小範疇的範疇中的態射。 在函子範疇中,態射是自然變換。參考...
