同態系統(homomorphic system) 通過非線性變換將非線性組合信號變換為線性組合,便於進行線性處理的一類系統的總稱。
基本介紹
- 中文名:同態系統
- 外文名:homomorphic system
- 套用學科:通信
定義
 圖1
圖1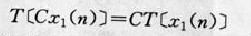 圖1
圖1 圖3
圖3 圖4
圖4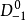
同態變換
同態濾波
乘法同態系統
卷積同態系統
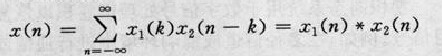 圖5
圖5 圖6
圖6 圖7
圖7同態系統(homomorphic system) 通過非線性變換將非線性組合信號變換為線性組合,便於進行線性處理的一類系統的總稱。
 圖1
圖1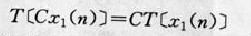 圖1
圖1 圖3
圖3 圖4
圖4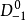
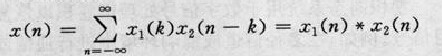 圖5
圖5 圖6
圖6 圖7
圖7同態系統(homomorphic system) 通過非線性變換將非線性組合信號變換為線性組合,便於進行線性處理的一類系統的總稱。...
假設M,M′是兩個乘集,也就是說M和M′是兩個各具有一個封閉的具有結合律的運算*與*‘的代數系統。σ是M射到M′的映射,並且任意兩個元的乘積的像是這兩個...
卷積同態系統(homomorphic system for con-volution)一種特定的數位訊號處理系統.它是專門處理卷積組合信號的同態系統.卷積同態系統在去混響和地質勘探中已經獲得重要...
乘法同態系統(multiplicative homomorphic system)輸入信號組合和輸出信號組合均為運算乘,取冪,並服從廣義疊加定理的系統。...
卷積同態系統(homomorphic system for convolution) 輸入信號組合和輸出信號組合均為卷積運算,並且服從廣義疊加定理的同態系統。...
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。群是數學最重要的概念之一,已滲透到現代數學的所有分支及其他學科中。...
交叉同態(crossed homomorphism)亦稱導映射,一種特殊的映射。設M是左G模,f:G→M是一個映射。若對任意σ,τ∈G,都有f(στ)=σf(τ)+f(σ),則稱映射f...
如果系統的輸入和輸出解釋為矢量空間中的矢量,運算規則□和〇對應於矢量加法,則系統變換H〔·〕就是代數上從輸入矢量空間到輸出矢量空間的一種線性變換,稱為同態...
同態與同構,是近世代數系統中的概念,是學習其他相關課程的基礎概念。...... 同態與同構,是近世代數系統中的概念,是學習其他相關課程的基礎概念。中文名 同態與同構...
霍普夫代數是20世紀60年代以後迅速發展起來的代數學的新學科。域k上的霍普夫代數是同時具有k代數結構和它的對偶結構(k余代數結構)並滿足一定的相容條件的代數系統。...
雙同態(bihomomorphism)是一種特殊的同態。指雙模之間的同態。設G與G’是兩個群,如果有一個由G到G’的映射σ,使σ (ab)=σ(a)σ(b)對所有的a,b∈G都...
同態濾波是一類特殊的非線性系統,它遵從廣義的疊加原理。在代數上,這類系統用輸入和輸出的矢量空間之間的線性變換來表征。...
一般系統論是關於任意系統研究的一般理論和方法。它雖源於理論生物學中的生物機體論,但其與哲學密切相關,是處於具體科學與哲學之間,具有橫斷科學性質的一種基本理論...
預測系統是由預測者、預測信息、預測手段、預測對象各要素及其相互作用構成的預測活動和過程。預測過程是:預測者根據決策需要確定預測對象;蒐集、整理、加工有關預測...
計算機信息系統,是指由計算機及其相關的和配套的設備、設施(含網路)構成的,按照一定的套用目標和規則對信息進行採集、加工、存儲、傳輸、檢索等處理的人機系統。即...
