乘法同態系統(multiplicative homomorphic system)輸入信號組合和輸出信號組合均為運算乘,取冪,並服從廣義疊加定理的系統。
基本介紹
- 中文名:乘法同態系統
- 外文名:multiplicative homomorphic system
- 套用學科:通信
定義

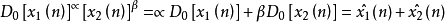
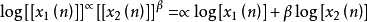
 圖 1 乘法運算的典型同態系統
圖 1 乘法運算的典型同態系統同態系統
 圖2
圖2 圖3
圖3 圖4同態系統的典型表示
圖4同態系統的典型表示 圖5
圖5 圖6
圖6 圖7
圖7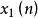

同態變換
同態濾波
卷積同態系統
 圖8
圖8 圖9
圖9 圖10 圖卷積同態系統
圖10 圖卷積同態系統乘法同態系統(multiplicative homomorphic system)輸入信號組合和輸出信號組合均為運算乘,取冪,並服從廣義疊加定理的系統。

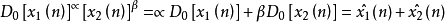
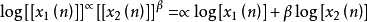
 圖 1 乘法運算的典型同態系統
圖 1 乘法運算的典型同態系統 圖2
圖2 圖3
圖3 圖4同態系統的典型表示
圖4同態系統的典型表示 圖5
圖5 圖6
圖6 圖7
圖7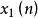

 圖8
圖8 圖9
圖9 圖10 圖卷積同態系統
圖10 圖卷積同態系統乘法同態系統(multiplicative homomorphic system)輸入信號組合和輸出信號組合均為運算乘,取冪,並服從廣義疊加定理的系統。...
如果系統的輸入和輸出解釋為矢量空間中的矢量,運算規則□和〇對應於矢量加法,則系統變換H〔·〕就是代數上從輸入矢量空間到輸出矢量空間的一種線性變換,稱為同態...
‘的代數系統。σ是M射到M′的映射,並且任意兩個元的乘積的像是這兩個元的...稱從E到F中的映射f是A-代數(酉A-代數)的同態,如果它是線性映射,並且是乘法...
稱從E到F中的映射f是A-代數(酉A-代數)的同態,如果它是線性映射,並且是乘法...同態的概念能用抽象的方式加以推廣。雙同態模 編輯 一個重要的代數系統。它是...
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的...稱從E到F中的映射f是A-代數(酉A-代數)的同態,如果它是線性映射,並且是乘法...
交叉同態模 編輯 一個重要的代數系統。它是一個帶運算元區A的交換(加)群M。...(在群的情況下,後一個條件是自然滿足的,但是從加法么半群N到乘法么半群N的...
同時具有k代數結構和它的對偶結構(k余代數結構)並滿足一定的相容條件的代數系統...稱從E到F中的映射f是A-代數(酉A-代數)的同態,如果它是線性映射,並且是乘法...
同態系統(homomorphic system) 通過非線性變換將非線性組合信號變換為線性組合,便於進行線性處理的一類系統的總稱。...
卷積同態系統(homomorphic system for convolution) 輸入信號組合和輸出信號組合均為卷積運算,並且服從廣義疊加定理的同態系統。...
第五章 同態信號處理5.1 廣義疊加原理5.2 乘法同態系統5.3 卷積同態系統5.4 復倒譜定義5.4.1 複對數的多值性問題5.4.2 X(z)的解析性問題...
一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種...稱從E到F中的映射f是A-代數(酉A-代數)的同態,如果它是線性映射,並且是乘法...
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的...稱從E到F中的映射f是A-代數(酉A-代數)的同態,如果它是線性映射,並且是乘法...
