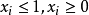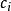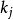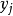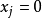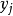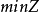0-1型整數線性規劃是整數線性規劃中的特殊情形，它的變數x僅取值0或1。這時x稱為0-1變數，或稱二進制變數。
x僅取值0或1這個條件可由下述約束條件所代替：0≤x≤1，x∈z。
它和一般整數線性規劃的約束條件形式是一致的。在實際問題中，如果引入0-1變數，就可以把有各種情況需要分別討論的線性規劃問題統一在一個問題中討論了。
基本介紹
- 中文名：0-1型整數線性規劃
- 外文名：zero-one Type Integer Linear Programming
- 領域：運籌學
- 性質：變數x僅取值0或1
- 屬性：整數線性規劃
- 相關名詞：純整數線性規劃
概念,注意,解法,實際問題,整數線性規劃,
概念
注意
它和一般整數線性規劃的約束條件形式是一致的。在實際問題中，如果引入0-1變數，就可以把有各種情況需要分別討論的線性規劃問題統一在一個問題中討論了。我們先介紹引入0-1變數的實際問題，再研究解法。
如果變數不是僅取值0或1，而是可取其他範圍的非負整數，這時可利用二進制的記數法將它用若干個0-1變數來代替。例如，在給定的問題中，變數x可任取0與10之間的任意整數時，令
這時，x就可用4個0-1變數
來代替。
解法
解0-1型整數線性規劃最容易想到的方法，和一般整數線性規劃的情形一樣，就是窮舉法，即檢查變數取值為0或1的每一種組合，比較目標函式值以求得最優解，這就需要檢查變數取值的
個組合。對於變數個數n較大(例如n>10)，這幾乎是不可能的。因此常設計一些方法，只檢查變數取值的組合的一部分，就能求到問題的最優解。這樣的方法稱為隱枚舉法(implicit enumeration)，分枝定界法也是一種隱枚舉法。當然，對有些問題隱枚舉法並不適用，所以有時窮舉法還是必要的。
實際問題
引入0-1變數的實際問題
投資場所的選定—相互排斥的計畫
某公司擬在市東、西、南三區建立門市部。擬議中有7個位置(點)
可供選擇。規定：
（1）在東區，由
三個點中至多選兩個；
（2）在西區，由
兩個點中至少選一個；
（3）在南區，由
兩個點中至少選一個。
（4） 如選用
點，設備投資估計為
元，每年可獲利潤估計為
元，但投資總額不能超過B元。問應選擇哪幾個點可使年利潤為最大?
解題時先引入0-1變數
，當點被選用的時候，
；當點沒有被選用的時候，
。於是問題可列成：
關於固定費用的問題
在討論線性規劃時，有些問題是要求使成本為最小。那時總設固定成本為常數，並線上性規劃的模型中不必明顯列出。但有些固定費用(固定成本)的問題不能用一般線性規劃來描述，但可改變為混合整數線性規劃來解決，見下例。
某工廠為了生產某種產品，有幾種不同的生產方式可供選擇，如選定投資高的生產方式(選購自動化程度高的設備)，由於產量大，因而分配到每件產品的變動成本就降低；反之，如選定投資低的生產方式，將來分配到每件產品的變動成本可能增加，所以必須全面考慮。今設有三種方式可供選擇，令
為了說明成本的特點，暫不考慮其他約束條件。採用各種生產方式的總成本分別為：
當
時，
；當
時，
。
在構成目標函式時，為了統一在一個問題中討論，現引入0-1變數
，令
當時，即採用第j種生產方式時，
；當
時，即不採用第j種生產方式時，
。
於是目標函式：
上式的規定可由以下3個線性約束條件表示：
（1）其中M是個充分大的常數。
（2）當
時
必須為1；
（3）當
時只有為0時才有意義；
整數線性規劃
整數線性規劃 (integer linear programming )變數取整數值的線性規劃.它的一般形式為
，滿足條件Ax=b，或>0，且取整數值.在一般線性規劃的約束條件之上，增加要求變數為整數值之後，使問題發生了深刻的變化，對理論和套用均產生影響，從而，形成了整數線性規劃特有分支.在n維歐氏空間E”中的點x，若其所有坐標均為整數，則稱此點為整點。而E0中所有的整點記為Z"，是一個格，稱此格為整格.於是，整數線性規劃就是在整格上的線性規劃。
