基本介紹
- 中文名:高德納箭號表示法
- 外文名:Knuth's up-arrow notation
- 發明人:高德納
- 發明時間:1976年
概念
定義
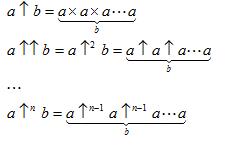
計算
一個箭頭
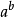
兩個箭頭
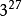
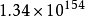
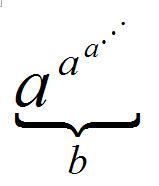 a↑↑b
a↑↑b三個箭頭
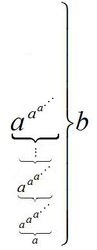
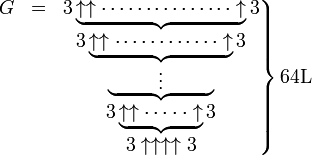
葛立恆數

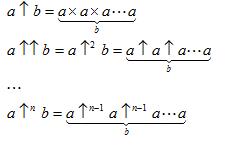
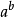
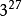
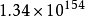
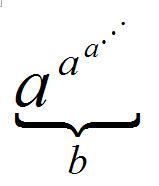 a↑↑b
a↑↑b

高德納箭號表示法是種用來表示很大的整數的方法,由高德納於1976年設計。它的意念來自冪是重複的乘法,乘法是重複的加法。n個箭頭代表(n+2)級超運算,如4↑↑2=4...
康威鏈式箭號表示法,是由約翰·何頓·康威發明的,用來表示大數。形式上看起來會像這樣:2→3→4→5→6。...
1 簡介 2 大數(數學) ▪ 大數記號 3 高德納箭號表示法 4 參見 斯坦豪斯-莫澤表示法簡介 編輯 斯坦豪斯-莫澤表示法,又稱斯坦豪斯-莫澤記號、斯坦豪斯...
不過,它可以通過利用高德納箭號表示法的遞歸公式來描述。雖然這個準確答案未知,但葛立恆數是現時所知最小的上界。雖然這個數太大了而無法完全計算出,但葛立恆數的...
即使這樣,古戈爾普勒克斯仍是小於一些特別定義出來的巨大數,比如用高德納箭號表示法或施泰因豪斯-莫澤記法表示的數。更簡單的,可以用比古戈爾普勒克斯少的符號數目...
使用高德納箭號表示法可將超運算運算元表示為(n-2)個箭頭。V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:2次歷史版本 最近更新: w_ou 突出貢獻榜 天問6254 ...
用高德納箭號表示法可以將超運算定義為注意到,對於序列的前三項有:通過這樣的遞歸能夠定義出高階運算,從而輸入很小的數就可以產生非常大的數。 [1] 其實,某一...
即使這樣,古戈爾普勒克斯仍是小於一些特別定義出來的巨大數,比如用高德納箭號表示法或施泰因豪斯-莫澤記法表示的數。更簡單的,可以用比古戈爾普勒克斯少的符號數目...
,也可視為超運算,記為n[3]m,亦可以用高德納箭號表示法,寫成n↑m,讀作“n的m次方”。 當指數為1時,通常不寫出來,因為運算出的值和底數的數值一樣;指數為...
當不能用上標時,例如在程式語言或電子郵件中,通常寫成n^m或n**m,亦可以用高德納箭號表示法,寫成 ,讀作“n的m次方”或者n的m次冪。...
