葛立恆數曾經被視為在正式數學證明中出現過最大的數,後來則被TREE(3)取代。
基本介紹
- 中文名:葛立恆數
- 外文名:Graham's Number
- 性質:拉姆齊理論問題
- 發現人:葛立恆
- 現知下限:12
術語簡介,作者簡介,葛立恆問題,上下界,最後500位,
術語簡介
葛立恆數,被視為現在正式數學證明中出現過最大的數。它大得連科學記數法也不夠用。
作者簡介
葛立恆問題
葛立恆數是拉姆齊理論(Ramsey theory)中一個極其異乎尋常問題的上限解,是一個難以想像的巨型數。這個問題表述為:
連線n維超立方體的每對幾何頂點,獲得一個有著2^n個頂點的完全圖(每對頂點之間都恰連有一條邊的簡單圖)。將該圖每條邊的顏色填上紅色或藍色。那么,使所有填法在四個共面頂點上包含至少一個單色完全子圖的最小n值為多少?
葛立恆數無比巨大,無法用科學記數法表示,就連a^(b^(c^(…)))這樣的指數塔形式也無濟於事,甚至連數學家都難以理解它。
舉個例子,如果把宇宙中所有已知的物質轉換成墨水,並把它放在一支鋼筆中,那也沒有足夠的墨水在紙上寫下所有這個數的位數。
事實上,這隻鋼筆甚至無法寫出這個數的位數的位數。就是在添加多少個“的位數”也無濟於事。
事實上,我們甚至無法寫出在後面要添加多少個“的位數”才能被這隻鋼筆寫出來。
不過,它可以通過利用高德納箭號表示法的遞歸公式來描述。
雖然這個準確答案未知,但葛立恆數是現時所知最小的上界。
雖然這個數太大了而無法完全計算出,但葛立恆數的最後幾位數可以通過簡單的算法導出。其最後12位數是262464195387。
那么,葛立恆問題的答案是多少?根據一些數學家的看法,他們懷疑答案是“6”。
上下界
定義函式f(n) = hyper(3,n+2,3) = 3→3→n(參看hyper運算符或康威鏈式箭號表示法),使用函式冪,則葛立恆數是f64(4)。
雖然葛立恆數不可以用康威鏈式箭號表示法很方便地表達,但康威鏈式箭號表示法能為它簡單地定上下界: 3→3→64→2 < 葛立恆數 < 3→3→65→2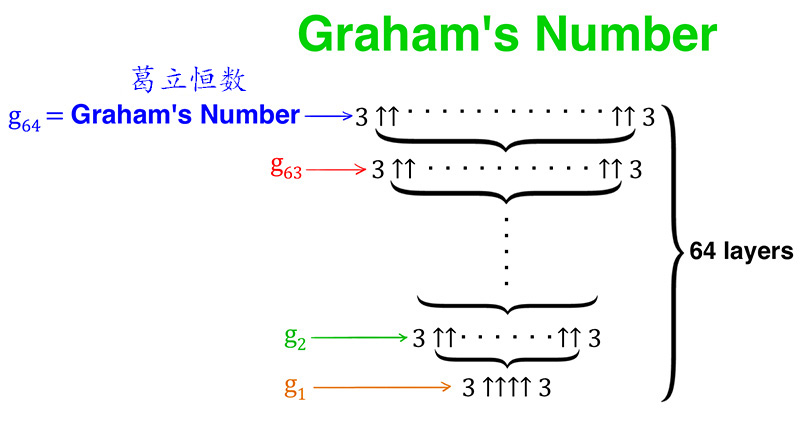

最後500位
葛立恆數的最後500位是:
02425 95069 50647 38395 65747 91365 19351 79833 45353 62521
43003 54012 60267 71622 67216 04198 10652 26316 93551 88780
38814 48314 06525 26168 78509 55526 46051 07117 20009 97092
91249 54437 88874 96062 88291 17250 63001 30362 29349 16080
25459 46149 45788 71427 83235 08292 42102 09182 58967 53560
43086 99380 16892 49889 26809 95101 69055 91995 11950 27887
17830 83701 83402 36474 54888 22221 61573 22801 01329 74509
27344 59450 43433 00901 09692 80253 52751 83328 98844 61508
94042 48265 01819 38515 62535 79639 96189 93967 90549 66380
03222 34872 39670 18485 18643 90591 04575 62726 24641 95387

