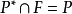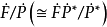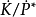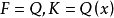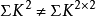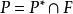高層序域實閉包

高層序域的實閉包(real closure of an ordered field of higher level)是指序域的實閉包在高層序域上的推廣。這類實閉包保留普通實閉包的一些特性，但在某些方面有別於普通實閉包。

基本介紹

• 中文名：高層序域的實閉包
• 外文名：real closure of an ordered field of higher level
• 所屬學科：數學
• 所屬問題：域論與伽羅瓦理論(序域)
• 相關概念：序域的實閉包，序閉包等

基本介紹

設是一個高層序域，的一個實閉包是指域F的一個極大代數擴張R，使得P在R上有忠實擴張。高層序域的實閉包總是存在的。此外，若R是的一個實閉包，則P在R上只有惟一的忠實擴張，然而不同於普通實閉包，恰好層大於1的序域的任意兩個實閉包未必F同構，至於如何判別兩個實閉包是否F同構，有下面的結論：高層序域的兩個實閉包與是F同構，若且唯若對於任何自然數m，

上面的結論實際上蘊含著普通實閉包的惟一性。

相關概念

高層序

高層序(ordering of higher level)是域的序(正錐)概念的推廣，它引起人們對域中元素的偶次冪方和的討論，從而導致出廣義的阿廷-施賴埃爾理論。高層序由貝克爾(E.Becker)首先引進並加以研究，從而獲得一系列結果。對於自然數n，域F的一個n層序是一個滿足下列條件的子集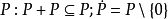是乘法群的一個子群，使得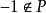且商群是循環群，其階能整除2n。1層序即為普通的序，凡層序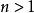者，統稱高層序。在上面的情況中，若商群的階為2m，其中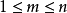，則稱P是域F的一個恰好m層序。當域F有一個(恰好)n層序P時，常稱是一個(恰好)n層序域。對於一個域是否有高層序這一問題，貝克爾證明了下面的結果：

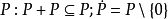
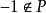
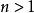
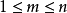
1.域F具有n層序，若且唯若F是形式n實的(formally n-real)，即不存在形如的等式，若且唯若F在通常意義下是形式實的。

2.域F具有恰好層序，若且唯若F是實的，並且，此處k是某個大於1的自然數。

平行於高層序這一概念，可相應地引入高層亞序等概念，並有相應的結果。

高層序的忠實擴張

高層序的忠實擴張(faithful extension of an ordering of higher level)是高層序域保持恰好層的擴張。設是一個高層序域，K是F的一個域擴張，若K有一個高層序，使得，則稱是P在K上的一個擴張，或稱是的一個(高層)序擴張，此時，由於可嵌入群中，所以P的恰好層不超過的恰好層。一般地，兩個恰好層未必相等，例如，設，其中x是有理數域Q上的未定元，由於，所以。由貝克爾(E.Becker)的結論，對於大於1的任意自然數m，K總有恰好m層序，然而只能是通常的序。對於上面的情況，若P的恰好層等於P*的恰好層，則稱P*是P在K上的一個忠實擴張，或稱是的一個忠實擴張。