基本介紹
- 中文名:序域
- 外文名:ordered field
- 簡介:有序結構的域
- 所屬學科:數學
- 所屬問題:域論(序域)
基本介紹

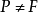


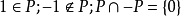

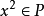













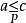




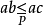

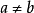
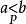
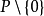
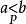
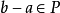



相關概念與定理
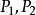




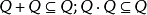
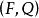







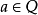





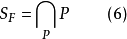
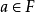
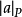
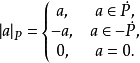


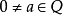
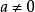

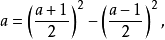

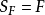

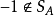

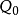


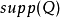


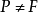


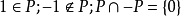

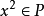













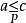




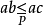

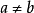
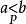
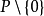
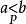
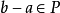



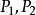




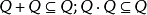
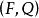







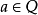





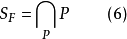
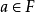
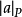
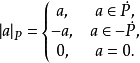


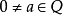
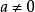

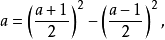

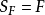

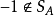

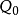


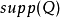
序域(ordered field)是一種特殊的域,它是有序結構的域。一個域F,若在它的元素之間存在一個二元關係>,滿足下述條件:1.對於任意a∈F,必有a=0或a>0或-a>...
高層序域的實閉包(real closure of an ordered field of higher level)是指序域的實閉包在高層序域上的推廣。這類實閉包保留普通實閉包的一些特性,但在某些方面...
子域上阿基米德序域(Archimedean orderedfield over a subfield)是一類相對於子域具有特殊性質的序域。...
稱滿足公理組I的集為域;滿足公理組I與II的集為有序域;滿足公理組I,II與(III)(1)的集為阿基米德有序域;滿足公理組I~III的集為完備阿基米德有序域或完備有...
這個完備性的意思非常接近採用戴德金分割來構造實數的方法,即從(有理數)有序域出發,通過標準的方法建立戴德金完備性。這兩個完備性的概念都忽略了域的結構。然而...
在同構的意義下,有且僅有一個完全有序域,即實數。完備性數理邏輯 編輯 在數理邏輯(en:mathematical logic中),一個理論(theory)被稱為完備的,如果對於其語言(...
矩陣格序環(matrix lattice-ordered ring)具有格序結構的矩陣環.設風(K)是序域K上n階全陣環,若定義(<a;;)axn<
阿基米德序(Archimedean ordering)一種重要的序.設>是域F的一個序,a>0是F中任一元.若對於F中每個b>0,總有某自然數n(與a,b有關),使得有na >b成立,則...
稱滿足公理組I的集為域;滿足公理組I與II的集為有序域;滿足公理組I,II與(III)(1)的集為阿基米德有序域;滿足公理組I~III的集為完備阿基米德有序域或完備有...
實數系(real number system)亦稱實數連續統.即所有實數的集合.任何一個完備的阿基米德有序域均可稱為實數系.在保序同構意義下它是惟一的,常用R表示.由於R是定義...
非降序列是一種特殊的數列。通常非降序列的元素定義在有序域上,每一項不小於它的前一項。非降序列通常指無窮序列。 例如:定義在實數域上的非降序列 1,2,3,4...
阿廷-施賴埃爾定理(Artin-Schreier theorem )序域實閉包的序同構性定理.對於任何一個序域(F,>),它所有的實閉包都是互為序同構的,換言之,除序同構不計外,序...
.NET平台下,程式集並沒有直接載入進進程中(傳統的Win32程式是直接承載的)。.NET可執行程式承載在進程的一個邏輯分區中,術語稱套用程序域(簡稱AppDomain)。一個...
.Net Remoting提供了一種允許一個套用域中的對象與另一個套用域中的對象進行互動的框架。是.NET框架中的一個重要技術改進,它用於減輕運行應用程式的系統開銷...
本書介紹了.NET Framework應用程式開發的重要主題,內容包括框架基礎,輸入和輸出,文本搜尋,集合與泛型,序列化,圖形處理,執行緒,套用程序域和服務,[2] 安裝和配置套用...
裝入程序域提供了在一組進程的同一虛擬地址中裝入共享庫的方法。裝入程式共享庫文本區域 系統裝入程式將共享庫裝入到多個全局共享庫區域內。一個區域稱為共享庫文本...
