基本介紹
- 中文名:序域
- 外文名:ordered field
- 簡介:有序結構的域
- 所屬學科:數學
- 所屬問題:域論(序域)
基本介紹

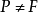


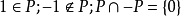

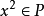













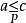




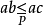

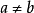
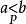
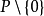
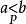
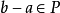



相關概念與定理
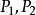




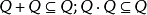
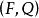







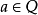





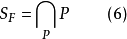
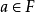
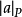
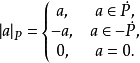


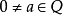
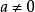

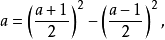

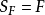

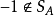

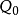


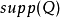


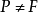


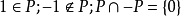

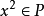













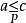




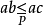

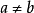
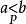
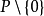
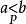
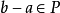



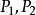




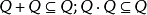
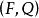







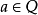





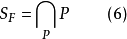
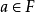
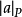
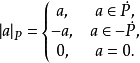


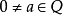
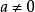

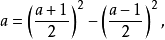

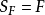

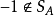

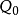


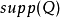
序域(ordered field)是一種特殊的域,它是有序結構的域。一個域F,若在它的元素之間存在一個二元關係>,滿足下述條件:1.對於任意a∈F,必有a=0或a>0或-a>...
高層序域的實閉包(real closure of an ordered field of higher level)是指序域的實閉包在高層序域上的推廣。這類實閉包保留普通實閉包的一些特性,但在某些方面...
子域上阿基米德序域(Archimedean orderedfield over a subfield)是一類相對於子域具有特殊性質的序域。...
稱滿足公理組I的集為域;滿足公理組I與II的集為有序域;滿足公理組I,II與(III)(1)的集為阿基米德有序域;滿足公理組I~III的集為完備阿基米德有序域或完備有...
任何一個完備的阿基米德有序域均可稱為實數系。在保序同構意義下它是惟一的,常用R表示。由於R是定義了算數運算的運算系統,故有實數系這個名稱。 實數可以用來...
在同構的意義下,有且僅有一個完全有序域,即實數。完備性數理邏輯 編輯 在數理邏輯(en:mathematical logic中),一個理論(theory)被稱為完備的,如果對於其語言(...
矩陣格序環(matrix lattice-ordered ring)具有格序結構的矩陣環.設風(K)是序域K上n階全陣環,若定義(<a;;)axn<
稱滿足公理組I的集為域;滿足公理組I與II的集為有序域;滿足公理組I,II與(III)(1)的集為阿基米德有序域;滿足公理組I~III的集為完備阿基米德有序域或完備有...
實數系(real number system)亦稱實數連續統.即所有實數的集合.任何一個完備的阿基米德有序域均可稱為實數系.在保序同構意義下它是惟一的,常用R表示.由於R是定義...
非降序列是一種特殊的數列。通常非降序列的元素定義在有序域上,每一項不小於它的前一項。非降序列通常指無窮序列。 例如:定義在實數域上的非降序列 1,2,3,4...
.NET平台下,程式集並沒有直接載入進進程中(傳統的Win32程式是直接承載的)。.NET可執行程式承載在進程的一個邏輯分區中,術語稱套用程序域(簡稱AppDomain)。一個...
本書介紹了.NET Framework應用程式開發的重要主題,內容包括框架基礎,輸入和輸出,文本搜尋,集合與泛型,序列化,圖形處理,執行緒,套用程序域和服務,[2] 安裝和配置套用...
