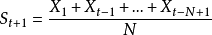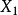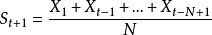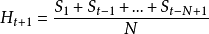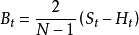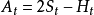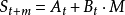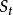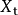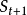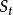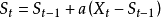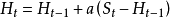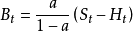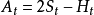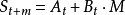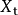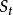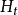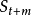預測計算是指在預測過程中根據預測模型通過數學方法求出初步預測結果的具體運算。
預測計算是預測一般程式中繼建立預測模型之後的不可缺少的一步，是產生預測結果的具體途徑，對預測結果有著直接影響。預測計算必須認真仔細，精確無誤。
對初步求得的預測結果，要考慮到模型中沒有包括的因素，對預測數值進行必要的調整，務求預測結果儘可能與實際相符合。
基本介紹
- 中文名：預測計算
- 外文名：Prediction calculation
- 定義：根據預測模型求出初步預測結果
- 套用學科：計算機原理
- 分類：計算機預測計算，人工預測計算
- 程式要求：有效性，靈活性，使用方便
定義,預測計算程式要求,有效性,靈活性,使用方便,常用的預測計算程式,移動平均法,二重移動平均法,指數平滑法,二重指數平滑法,自適應過濾法,邏輯斯諦曲線法,龔柏茲曲線法,傳統分解法,馬爾柯夫分析法,多元線性回歸法,
定義
預測計算是指在預測過程中根據預測模型通過數學方法求出初步預測結果的具體運算。
預測計算是預測一般程式中繼建立預測模型之後的不可缺少的一步，是產生預測結果的具體途徑，對預測結果有著直接影響。預測計算必須認真仔細，精確無誤。
對初步求得的預測結果，要考慮到模型中沒有包括的因素，對預測數值進行必要的調整，務求預測結果儘可能與實際相符合。
與人工預測相比，計算機預測的優勢是耗時短，對於計算比較繁瑣的正適合由計算機去進行。特別是安全控制所需要的短期和超短期負荷預測，由於實時性的要求，只有用計算機處理才來得及，人工計算是不行的。但是，因為一些特殊因素難以建立模型，只有憑經驗人工加以修正，計算機則無法做到。如果今後都能總結出規律，有了模型，計算機也就可以處理了。所以，目前人工預測比較準確，計算機預測則誤差大些。
預測計算程式要求
有效性
預測程式包的目的全在於套用．所以，程式包所選擇的模型和方法，應充分考慮其工作效率和先進性。
靈活性
預測程式包不僅可以供操作人員對裝入的各項預測計算程式進行選擇，還應提供預測人員對預測過程進行干預的手段。同時，預測程式包還應具有一定的可塑性，可以適應不同用戶的要求以及對未來的發展情況進行修改與補充。
使用方便
作為一種面向用戶的套用軟體，其操作應力求簡單，應儘量減少輔助操作，使具有一般預測知識的人都可以使用。
根據上述要求，預測計算程式包應將不同的預測計算程式做為分枝程式進行處理。把各種預測計算程式編製成相互獨立的分程式運行比較靈活。這樣設計，便於對計算程式包進行增加、刪除和修改，操作人員只需按選單提示進行選擇，就能進行正確的預測計算。
在程式設計中，對於同類型的計算程式儘可能地套用統一的輸入輸出格式。這樣雖然占的記憶體容量大一些，但是一組輸入數據可以調用幾種不同的預測計算程式，便於切換，便於進行對比分析。同時，採用設定輸入多種參數和特徵值的方式，使預測人員能夠根據實際情況對模型不斷地進行調整和修正，實現人機對話。
常用的預測計算程式
移動平均法
移動平均法是取一組觀察值，求出其平均值，然後用該平均值作為下期預測值。它是一種平滑預測值，適用於即期一短期預測，數據樣式為水平型，‘採用時間數列模型，預測模型為
。
其中
為時間為t+1的預測值；
為時間為t的實際值；N為包含在平均數中的數值個數。
二重移動平均法
二重移動平均法是取一組單重平均數，然後用此組平均數來計算另一組移動平均數。它是一種高級平滑預測法，適用於即期、短期預測，數據樣式可為季節型、趨勢型。預測模型如下：
其中，
為預測值，
為實際值，N為包含在平均數中的數值個數，M為未來期數。
指數平滑法
指數平滑法是對一組觀察值，給出以指數遞減的權數集。在計算新的預測值時，只需要有近期的觀察值，近期的預測值和一個a值。它是一種平滑預測法，適用於即期、短期預測，數據樣式為水平型，採用時間序列模型。預測模型為
其中a為平滑參數，
為時間為t+1的預測值，
為時間為t的預測值，
為時間為t的實際值。
二重指數平滑法
二重指數平滑法是用單重指數平滑值，來計算另一個指數平滑值，再求二者的差值，將差值加回單重指數平滑值上，作為預測值。它是一種高級平滑預測法，適用於即期．短期預測，數據樣式可為季節型，趨勢型。預測模型如下：
自適應過濾法
自適應過濾法是一種控制預測法(也可以認為是一種高級平滑預測法)，用的數學模型為時間序列模型，適用於近期、短期、中期預測，數據樣式為水平型、趨勢型、季節型，循環型。它可以根據一組歷史數據自動調整權值，選定一組最佳權值，進行預測，還可以用於修勻一組預測數據。
它調整權值的原理為：先給定一權值，然後計算這次預測誤差，根據此誤差可調整權值．通過反覆疊代，直到均方誤差達到達到最小時的權值，即為最佳一組權值。
邏輯斯諦曲線法
邏輯斯諦曲線法適用於預測成長曲線拐向飽和值的階段。數學模型為時間序列模型，適用於耐消費商品的中期、長期預測。
龔柏茲曲線法
龔柏茲曲線法適用於預測成長曲線的迅速增長階段。數學模型為時間序列模型，適用於中期、長期預測。計算的步驟是先把一組觀察值等分成三組，每組包含N個值，對每個觀察值取對效，然後按下面的數學模型來進行預測計算。
傳統分解法
傳統分解法特別適用於進行季節商品的短、中期預測。數據樣式為非自相關的趨勢型，水平型，季節型，循環型。數據個數最低為5(季)個，模型為時間序列類型。
馬爾柯夫分析法
馬爾柯夫分析法是一種機率預測法，適用於商業中的市場占有率和期望利潤的預測。馬爾柯夫過程分析是一種動態隨機數學模型，它建立在系統“狀態"和“狀態轉移”的概念上。
多元線性回歸法
多元線性回歸法用於多個經濟變數之間呈直線因果關係的預測。數學模型可為時間數列、因果型及統計型，數據樣式為非自相關趨勢型，用於短期，中期及長期預測。
