目前，對一般的非線性濾波問題的研究相當活躍，常用的非線性濾波有擴展卡爾曼濾波(EKF)、不敏卡爾曼濾波(UKF)、粒子濾波(PF)等。在實際套用中，非線性濾波算法的選取還應根據具體套用場合和條件，並需要在估計精度、實現難易程度、數值穩健性及計算量等各種指標之間綜合權衡。
基本介紹
- 中文名：非線性濾波
- 外文名：nonlinear filtering
- 套用：數位訊號處理
- 代表：中值濾波；粒子濾波；卡爾曼濾波
概念,分類,1.中值濾波,2.雙邊濾波,3.粒子濾波,4.卡爾曼濾波,套用,
概念
從連續的(或離散的)輸入數據中濾除噪聲和干擾以提取有用信息的過程稱為濾波，而相應的裝置稱為濾波器。根據濾波器的輸出是否為輸入的線性函式，可將它分為線性濾波器和非線性濾波器兩種。非線性濾波的原始數據與濾波結果是一種邏輯關係，即用邏輯運算實現，如最大值濾波器、最小值濾波器、中值濾波器等，是通過比較一定鄰域內的灰度值大小來實現的，沒有固定的模板，因而也就沒有特定的轉移函式，另外，膨脹和腐蝕也是通過最大值、最小值濾波器實現的。
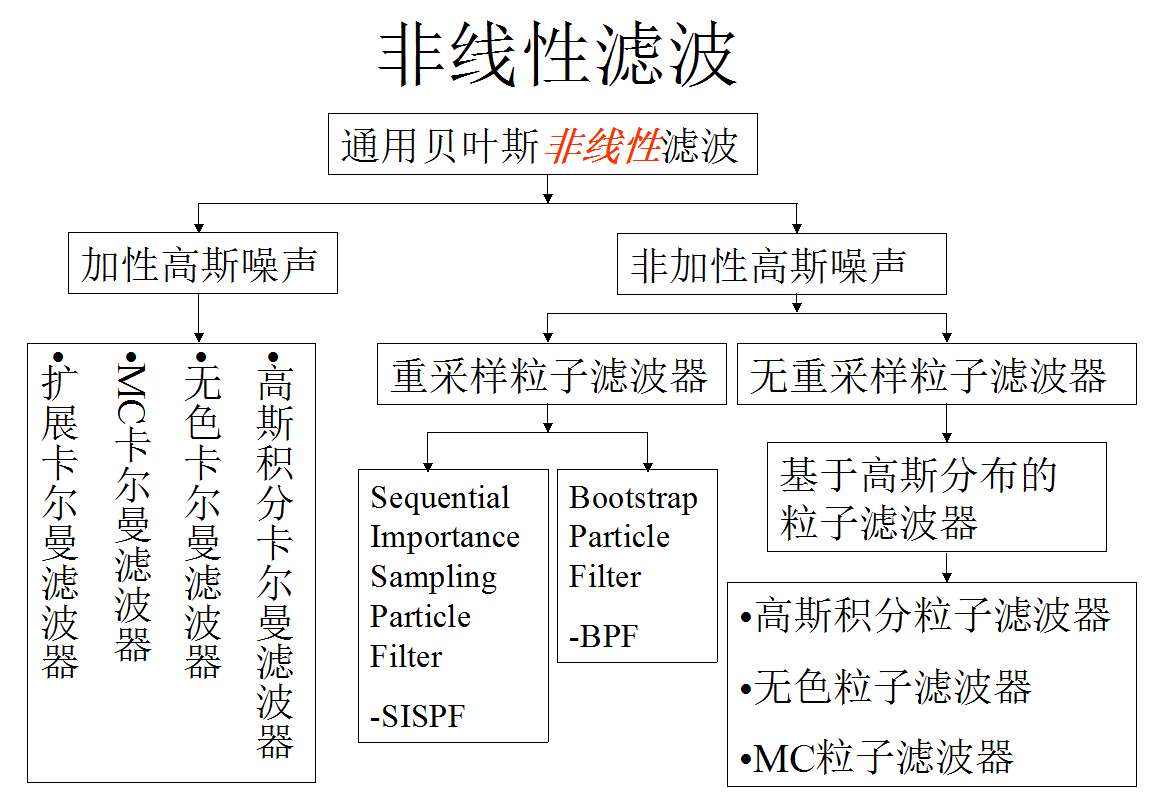
目前，對一般的非線性濾波問題的研究相當活躍，常用的非線性濾波有擴展卡爾曼濾波(EKF)、不敏卡爾曼濾波(UKF)、粒子濾波(PF)等。
一般的非線性最優濾波可歸結為求條件期望的問題。對於有限多個觀測值的情形，條件期望原則上可以用貝葉斯公式來計算。但即使在比較簡單的場合，這樣得出的結果也是相當繁雜的，無論對實際套用或理論研究都很不方便。與卡爾曼濾波類似，人們也希望能給出非線性濾波的某種遞推算法或它所滿足的隨機微分方程。但一般它們並不存在，因此必須對所討論的過程X與Y加以適當的限制。非線性濾波的研究工作相當活躍，它涉及隨機過程論的許多近代成果，如隨機過程一般理論、鞅、隨機微分方程、點過程等。其中一個十分重要的問題，是研究在什麼條件下，存在一個鞅M，使得在任何時刻,M和Y 都包含同樣的信息；這樣的M稱為Y 的新息過程。目前對於一類所謂“條件正態過程”，已經給出了非線性最優濾波的可嚴格實現的遞推算式。在實際套用上，對非線性濾波問題往往採用各種線性近似的方法。
分類
1.中值濾波
中值濾波是基於排序統計理論的一種能有效抑制噪聲的非線性信號處理技術，其基本原理是把數字圖像或數字序列中一點的值用該點的一個鄰域中各點值的中值代替，讓周圍的像素值接近的真實值，從而消除孤立的噪聲點，對於斑點噪聲（speckle noise）和椒鹽噪聲（salt-and-pepper noise）來說尤其有用，因為它不依賴於鄰域內那些與典型值差別很大的值。中值濾波器在處理連續圖像窗函式時與線性濾波器的工作方式類似，但濾波過程卻不再是加權運算。
中值濾波在一定的條件下可以克服常見線性濾波器如最小均方濾波、方框濾波器、均值濾波等帶來的圖像細節模糊，而且對濾除脈衝干擾及圖像掃描噪聲非常有效，也常用於保護邊緣信息, 保存邊緣的特性使它在不希望出現邊緣模糊的場合也很有用，是非常經典的平滑噪聲處理方法。
中值濾波的改進改進——加權中值濾波：在中值濾波的基礎上加以改進，其性能在一定程度上優於中值濾波。
中值濾波與均值濾波器比較
中值濾波器與均值濾波器比較的優勢：在均值濾波器中，由於噪聲成分被放入平均計算中，所以輸出受到了噪聲的影響，但是在中值濾波器中，由於噪聲成分很難選上，所以幾乎不會影響到輸出。因此同樣用3x3區域進行處理，中值濾波消除的噪聲能力更勝一籌。中值濾波無論是在消除噪聲還是保存邊緣方面都是一個不錯的方法。
2.雙邊濾波
雙邊濾波（Bilateral filter）是一種非線性的濾波方法，是結合圖像的空間鄰近度和像素值相似度的一種折衷處理，同時考慮空域信息和灰度相似性，達到保邊去噪的目的。具有簡單、非疊代、局部的特點。
雙邊濾波器的好處是可以做邊緣保存（edge preserving），一般過去用的維納濾波或者高斯濾波去降噪，都會較明顯地模糊邊緣，對於高頻細節的保護效果並不明顯。雙邊濾波器，顧名思義比高斯濾波多了一個高斯方差sigma－d，它是基於空間分布的高斯濾波函式，所以在邊緣附近，離的較遠的像素不會太多影響到邊緣上的像素值，這樣就保證了邊緣附近像素值的保存。但是由於保存了過多的高頻信息，對於彩色圖像里的高頻噪聲，雙邊濾波器不能夠乾淨的濾掉，只能夠對於低頻信息進行較好的濾波。
3.粒子濾波
由於自然界中的動態系統一般都為非線性非高斯分布，因此研究非線性非高斯分布情況下的濾波算法具有普遍意義。粒子濾波是針對此種情況下的濾波算法，它以貝葉斯估計理論為基礎，以蒙特卡羅隨機抽樣算法為核心，通過抽樣估計狀態空間的後驗機率密度分布，由時間更新與測量更新兩個步驟來達到最優貝葉斯估計。粒子濾波以序貫重要性採樣為核心算法（Sequential Importance Sampling，SIS），它是一種蒙特卡羅方法，它通過蒙特卡羅模擬實現遞推貝葉斯濾波，其核心思想是利用一系列隨機樣本的加權和表示所需的後驗機率密度，得到狀態的估計值。
為了解決粒子濾波較高的計算開銷的問題，現在有很多的改進方案，如粒子濾波與其它濾波算法結合的複合算法，也有從硬體上進行開發的方案。
4.卡爾曼濾波
卡爾曼濾波是一種高效率的遞歸濾波器（自回歸濾波器），它能夠從一系列的不完全及包含噪聲的測量中，估計動態系統的狀態。
卡爾曼濾波是一種遞歸的估計，即只要獲知上一時刻狀態的估計值以及當前狀態的觀測值就可以計算出當前狀態的估計值，因此不需要記錄觀測或者估計的歷史信息。卡爾曼濾波器與大多數濾波器不同之處，在於它是一種純粹的時域濾波器，它不需要像低通濾波器等頻域濾波器那樣，需要在頻域設計再轉換到時域實現。
卡爾曼濾波器的操作包括兩個階段：預測與更新。在預測階段，濾波器使用上一狀態的估計，做出對當前狀態的估計。在更新階段，濾波器利用對當前狀態的觀測值最佳化在預測階段獲得的預測值，以獲得一個更精確的新估計值。
套用
在實際套用中，非線性濾波算法的選取還應根據具體套用場合和條件，並需要在估計精度、實現難易程度、數值穩健性及計算量等各種指標之間綜合權衡。
例如，在雷達對再入飛行目標進行跟蹤問題中，由於目標再入速度極快,受到複雜的空氣動力影響而呈現出很強的非線性，通常用 UKF 方法更適合；但是如果再入飛行器的空氣動力特性已知(即彈道係數已知，則系統模型呈弱非線性，此時 EKF 效果優於 UKF；基於插值展開近似方法計算簡單、精度高、適應面廣、數值穩健性好，是一種很有發展前途的非線性估計方法；Un-scented濾波和粒子濾波用非線性變換代替傳統的線性變換，體現了非線性濾波算法應更接近系統的非線性本質的思想，代表了非線性濾波的發展方向。
