維納濾波

維納濾波（wiener filtering) 一種基於最小均方誤差準則、對平穩過程的最優估計器。這種濾波器的輸出與期望輸出之間的均方誤差為最小，因此，它是一個最佳濾波系統。它可用於提取被平穩噪聲污染的信號。

從連續的（或離散的）輸入數據中濾除噪聲和干擾以提取有用信息的過程稱為濾波，這是信號處理中經常採用的主要方法之一，具有十分重要的套用價值，而相應的裝置稱為濾波器。根據濾波器的輸出是否為輸入的線性函式，可將它分為線性濾波器和非線性濾波器兩種。維納濾波器是一種線性濾波器。

基本介紹

• 中文名：維納濾波
• 外文名：wiener filtering
• 構成：採用電感、電容等分立元件構成
• 優點：適應面較廣
• 要求：輸入過程是廣義平穩的
• 套用學科：通信

簡介

常用的濾波器是採用電感、電容等分立元件構成，如RC低通濾波器、LC諧振迴路等。但對於混在隨機信號中的噪聲濾波，這些簡單的電路就不是最佳濾波器，這是因為信號與噪聲均可能具有連續的功率譜。不管濾波器具有什麼樣的頻率回響，均不可能做到噪聲完全濾掉，信號波形的不失真。因此，濾波器研究的一個基本課題就是：如何設計和製造最佳的或最優的濾波器。所謂最佳濾波器是指能夠根據某一最佳準則進行濾波的濾波器。

基本原理

維納濾波理論是由數學家N．維納(Norbert Wiener ，1894~1964)於第二次世界大戰期間提出的。這一科研成果是這一時期重大科學發現之一，他提出了線性濾波的理論和線性預測的理論，對通信工程理論和套用的發展起了重要的作用。維納濾波就是為紀念他的重要貢獻而命名的。

維納濾波的基本原理是：設觀察信號y(t)含有彼此統計獨立的期望信號x(t)和白噪聲ω（t）可用維納濾波從觀察信號y(t)中恢復期望信號x(t)。設線性濾波器的衝擊回響為h(t)，此時其輸入y(t)為y(t)=x(t)+w(t)，輸出 為圖1.

圖1

從而，可以得到輸出 對x(t)期望信號的誤差為圖2

圖2

其均方誤差為圖3：

圖3

E[ ]表示數學期望。套用數學方法求最小均方誤差時的線性濾波器的衝擊回響h_opt(t)可得如圖4方程.

圖4

式中，R_yx(t)為y(t)與x(t）的互相關函式，R_yy(τ-σ)為y(t)的自相關函式。上述方程稱為維納-霍夫(Wiener-Hopf)方程。求解維納-霍夫方程可以得到最佳濾波器的衝擊回響h_opt(t)。在一般情況下，求解上述方程是有一定困難的，因此這在一定程度上限制了這一濾波理論的套用。然而，維納濾波對濾波和預測理論的開拓，影響著以後這一領域的發展。

要求

輸入過程廣義平穩

輸入過程的統計特性已知

效果

當信號和干擾以及隨機噪聲同時輸入該濾波器時，在輸出端將信號儘可能精確表現出來；

維納濾波根據全部過去觀測值和當前觀測值來估計信號的當前值，解形式是傳遞函式或單位脈衝回響，說白了就是一個IIR無限單位脈衝濾波器。

發展

20世紀40年代，維納奠定了關於最佳濾波器研究的基礎。即假定線性濾波器的輸入為有用信號和噪聲之和，兩者均為廣義平穩過程且知它們的二階統計特性，維納根據最小均方誤差準則(濾波器的輸出信號與需要信號之差的均方值最小)，求得了最佳線性濾波器的參數，這種濾波器被稱為維納濾波器。在維納研究的基礎上，人們還根據最大輸出信噪比準則、統計檢測準則以及其他最佳準則求得的最佳線性濾波器。實際上，在一定條件下，這些最佳濾波器與維納濾波器是等價的。因而，討論線性濾波器時，一般均以維納濾波器作為參考。維納濾波是40年代線上性濾波理論方面所取得的最重要的成果。

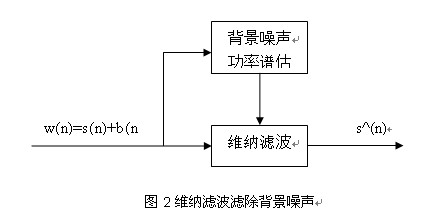維納濾波濾除背景噪聲

利用平穩隨機過程的相關特性和頻譜特性對混有噪聲的信號進行濾波的方法，1942年美國科學家N.維納為解決對空射擊的控制問題所建立。

基本概念

從噪聲中提取信號波形的各種估計方法中，維納（Wiener）濾波是一種最基本的方法，適用於需要從噪聲中分離出的有用信號是整個信號（波形），而不只是它的幾個參量。

設維納濾波器的輸入為含噪聲的隨機信號。期望輸出與實際輸出之間的差值為誤差，對該誤差求均方，即為均方誤差。因此均方誤差越小，噪聲濾除效果就越好。為使均方誤差最小，關鍵在於求衝激回響。如果能夠滿足維納－霍夫方程，就可使維納濾波器達到最佳。根據維納－霍夫方程，最佳維納濾波器的衝激回響，完全由輸入自相關函式以及輸入與期望輸出的互相關函式所決定。

優缺點

維納濾波器的優點是適應面較廣，無論平穩隨機過程是連續的還是離散的，是標量的還是向量的，都可套用。對某些問題，還可求出濾波器傳遞函式的顯式解，並進而採用由簡單的物理元件組成的網路構成維納濾波器。維納濾波器的缺點是，要求得到半無限時間區間內的全部觀察數據的條件很難滿足，同時它也不能用於噪聲為非平穩的隨機過程的情況，對於向量情況套用也不方便。因此，維納濾波在實際問題中套用不多。

基於Contosrcet域的維納濾波的圖像復原

實現維納濾波的要求是：

1.輸入過程是廣義平穩的

2.輸入過程的統計特性是已知的。根據其他最佳準則的濾波器亦有同樣要求

然而，由於輸入過程取決於外界的信號、干擾環境，這種環境的統計特性常常是未知的、變化的，因而難以滿足上述兩個要求。這就促使人們研究自適應濾波器。