非線性內模控制

非線性內模控制是指針對非線性系統的一種內模控制方法。

內模控制是一種基於過程數學模型進行控制器設計的新型控制策略。由於其設計方法簡單，控制性能良好，並且在系統分析方面具有一定的優越性，因此內模控制不僅是一種實用的先進控制算法，還是研究預測控制等基於模型的控制策略的重要理論基礎。

基本介紹

• 中文名：非線性內模控制
• 外文名：nonlinear internal model control
• 定義：非線性系統的一種內模控制方法
• 建模方法：傳統數學、神經網路模型等
• 特點：強魯棒性、實用性弱等
• 涉及領域：自動控制

簡介

與線性系統類似，非線性系統的內模控制結構如《非線性系統內模控制結構圖》所示。

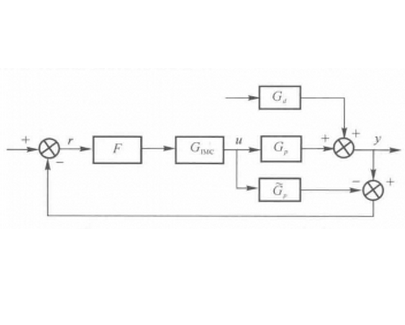
非線性系統內模控制結構圖

其中。Gp(s)為非線性對象，(s)為模型，(s)為控制器，F為濾波器，Gd(S)為擾動或模型不確定因素。

可以證明，線性內模控制的三個重要性質均可以推廣到非線性內模控制。但在非線性內模控制中，對象模型的獲取和控制器的設計遠比線性系統困難，利用經典的建模方法很難適應複雜非線性系統的建模需要。

系統的模型與對象並行運行，兩者之間的輸出誤差經濾波器作用後反饋給非線性內模控制器，控制器從模型獲取狀態，並不需要得到對象的狀態。若模型與對象完全匹配，且初始條件相同時，控制器將與傳統非線性系統反饋線性化的結果一致。

建模方法

傳統數學模型

傳統數學模型在內模控制中套用相當廣泛，特別是以傳遞函式表示的輸入、輸出模型幾乎統治了線性內模控制的研究。在非線性內模控制中，Henson(漢森)等研究了微分方程描述的仿射非線性對象和模型，Kendi(肯迪)等採用可因式分解的非線性運算元研究存在可測干擾和輸入飽和的仿射非線性系統。傳統數學模型可逆性容易判斷，模型可逆時能解析獲得模型的逆，能夠深入分析閉環系統的穩定性和魯棒性，但是很多複雜非線性對象是難以用數學模型表示的。

神經網路模型

神經網路內模控制方法充分利用了神經網路強大的函式逼近能力，在一定程度上克服了非線性系統難以建模的困難，受到人們的青睞。

(1)神經網路內模控制一般採用以下兩種方法：①兩個神經網路分別逼近模型和模型的逆；②採用神經網路逼近模型，然後用非線性最佳化方法數值求取控制量。這兩種方法固然可以獲得較高精度的模型，但是模型逆的精度卻往往得不到保證，這是因為獲得的神經網路模型可能是不可逆的。

(2)根據內模控制的性質可知，當控制器偏離模型的逆使得控制器和模型的穩態增益乘積不等於1時，會導致控制系統跟蹤階躍輸入出現靜差，因此基於神經網路的內模控制需要解決以下理論問題：①以網路拓撲結構表示的神經網路模型如何判斷其可逆性；②如果可逆，求逆的過程能否保證收斂；③能否求出一個高精度的模型逆。由此可見，非線性內模控制中模型可逆性的問題遠比線性內模控制中的複雜。神經網路模型求逆的問題已經有一些數值算法，但是目前還缺乏嚴格的理論依據，因而在一定程度上限制了神經網路內模控制的套用。

由於模型逆的精度對內模控制效果的影響遠大於模型精度所產生的影響，因此通過適當犧牲模型精度以確保模型可逆，並求得高精度的模型逆就成為解決非線性內模控制的一條可行之路。仿射模型的優點是模型逆可以解析獲得，從而逐漸吸引了研究者的注意。其中採用仿射形式的Hopfield(霍普菲爾德)網路來逼近對象的方法，可利用該網路的穩定性定理判斷模型和模型逆的穩定性；而另一種方法是基於雙BP網路(多層前饋神經網路，Back Propagation network)組成的仿射模型，提出針對非線性離散時滯系統的神經網路內模控制器的設計。然而，這些方法的缺點是對一般非線性系統的建模精度不高，比較適用於仿射非線性對象。

模糊系統模型

與神經網路相比，模糊系統的非線性函式逼近能力較晚為人們所認識，模糊模型最初套用於內模控制中所起的作用類似於神經網路輸入、輸出模型，因而也無法避免模型求逆的困難。但在Abonyi(奧博尼)和Edgar(艾德加)等的努力下，模糊模型求逆獲得了較好的結果。Abonyi針對一類特殊的兩輸人一輸出模糊系統提出了一種解析求逆的方法，並將結論推廣到MISO模型。Edgar提出一種特殊的模糊模型，其建模過程可以保證模型總是可逆的，並能夠在每個採樣時間內獲得精確的模型逆。另外，Fink(芬克)指出由於模糊系統建模過程是採用一系列線性模型加權平均來逼近非線性對象，因而模型求逆可以用局部線性模型求逆的加權平均來解析獲得，使得求逆過程的計算量大幅減少。可以預見，由於模糊神經網路結合了神經網路和模糊邏輯二者的優點，具有自學習和利用知識的能力，在一定情況下還可以解析獲得模型逆，因此作為內模控制建模工具的研究潛力很大。

Volterra級數模型

Volterra(沃爾泰拉)級數模型是一種重要的非線性系統模型，可以描述一大類工業對象。作為一種非參數模型，該模型的優點是可以通過系統輸入、輸出數據直接辨識得到，而不需要複雜的結構辨識過程。不過從模型辨識的角度看，Volterra級數需要相當多的被估計參數才能取得滿意的精度，這在很大程度上限制了這種方法的套用。

特點

非線性內模控制有機地結合了非線性反饋線性化技術與內模控制結構，系統不但對模型失配、參數變化及各種不確定性干擾具有強魯棒性，消除不確定性的影響，而且能夠很好地補償被控對象的非線性特性，從而取得優良的性能。

但是眾多的非線性內模控制方案很少套用於實際。實際控制時多採用計算機控制，需要將系統離散化，而離散化會帶來許多意想不到的問題，比如離散化引起的誤差若處理不當會對系統性能造成較大影響。