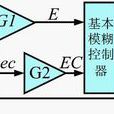
系統介紹
在研究沒有人參與的定量化的精確係統時,有一系列行之有效的系統理論;但在人機系統、管理系統、經濟系統、社會系統等與人的思維活動有某種聯繫的系統中,由於人腦的邏輯、推理、判斷、決策並非完全精確,這種與人有關的系統就具有某種模糊性。隨著電子數字計算機向智慧型機的方向發展,將出現越來越多的模糊系統。
在通常的系統理論中,一個系統在某一時刻的狀態和輸入一經決定,下一時刻的狀態和輸出就明確地唯一決定,這種系統稱為確定性系統,否則就稱為非確定性系統。假定給出系統某一時刻的狀態與輸入,儘管不能唯一決定下一時刻的狀態與輸出,但能決定下一狀態出現的機率分布,這種系統則稱為隨機系統,這是一類非確定性系統。如果不能決定下一狀態出現的機率分布,但可以確定下一時刻所有可能狀態的集合,這是另一類非確定性系統。如果把這種非確定性系統中可能狀態的集合用模糊集合來表示,就稱為模糊系統。
模糊邏輯基礎
模糊集合
人們的思維中的很多概念沒有明確的外延,如“大”、“中”、“小”等,這些模糊概念不能用經典集合加以描述。1965 年 Zadeh 教授提出用模糊集合來描述這些模糊概念,其定義如下:
給定論域 U,U 到[0,1]閉區間的任一映射
,
:U→[0,1],u→
。
稱為確定了 U 的一個模糊子集 A,
稱為模糊子集的隸屬函式,
稱為u 對於 A的隸屬度,反映了 u 對模糊子集 A的從屬程度,模糊子集也稱模糊集合。
隸屬度函式
常見的隸屬度函式有以下幾種類型:三角型函式(圖2)、梯型函式(圖2)、高斯型函式(圖3)、鐘型函式(圖3)、Sigmoid 型函式 (圖4)和Z 型函式(圖4)。
三角型函式和梯型函式本質上都是分段線性函式,因此使用和計算比較簡單。
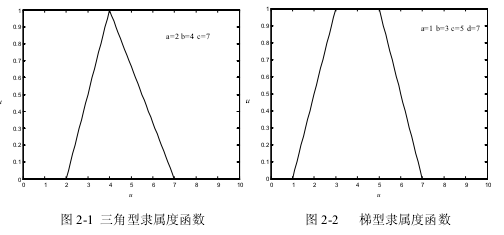 圖1
圖1高斯型隸屬度函式和鐘型隸屬度函式曲線都具有很好的光滑性,圖形沒有零點且具有比較清晰的物理意義,是最常用的隸屬度函式。
 圖2
圖2Sigmoid 型隸屬度函式曲線同樣有著很好的光滑性,與高斯型隸屬度函式等不同,Sigmoid 型隸屬度函式適合表示非對稱性的事物。Z 型隸屬度函式是基於樣條插值的。
 圖3
圖3基本架構
模糊系統的基本架構如圖1所示,其中,主要的功能方塊包括:模糊化機構、模糊規則庫、模糊推理引、以及去模糊化機構。
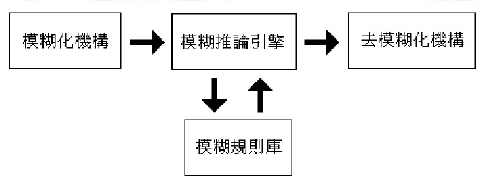 圖4模糊系統的基本架構
圖4模糊系統的基本架構模糊化機構
模糊化機構的功能是將明確的外界輸入數據轉換成適當的語言式模糊信息;也就是說將明確數據模糊化成模糊信息。
模糊規則庫
1、語言式模糊規則(Mamdani模糊規則):
2、函式式模糊規則:
(1)線性式模糊規則:
(2)單點式模糊規則:
(3)Tsukamoto模糊規則:此模糊規則的後件
採用的是用於單調性隸屬函式的模糊集合,因此,每一個模糊規則經過推理後,得到的是一個明確值。
推理引擎將藉由這些模糊規則來進行推理,以決定下一步驟所要採取的決定。以上三種規則的主要差別只在於模糊規則的後件有所不同而已。
模糊推理引
模糊推理引擎是模糊系統的核心,它可以藉由近似推理或模糊推理的進行,來仿真人類的思考決策模式,以達到解決問題的日地。
去模糊化機構
將經過模糊推理之後產生的結淪,轉換為一明確數值的過程,我們稱之為“去模糊化”。
由於不同的模糊規則所採用的後件會有所不同,囚此,經過模糊推理後所得到的結淪,有的是以模糊集合來表示(如語言式模糊規則),而有的是以明確數值來表示。
對於推理後是模糊集合的,常用的去模糊化方法有重心法、最大平均法、修正型最大平均法、中心平均法和修正型重心法等;對於推理後是明確數值的,權重式平均法是被最為廣泛使用的去模糊化方法。
特點
模糊系統的優點是可以融入專家經驗,且泛化能力受數據影響小。由於可以系統有效地利用語言形式的專家經驗,模糊推理系統已在諸多工程領域獲得了套用,然而目前的模糊邏輯系統的輸入全為精確值或全為模糊集合,在套用中可能需要能同時輸入精確值和模糊語言變數,這需要對現有的模糊系統進行改進;在模糊系統構建中輸入、輸出空間的劃分和隸屬度函式及其參數的確定主要依靠個人經驗,往往需要反覆試湊,具有很大的主觀性和不確定性。
模糊系統類型
純模糊邏輯系統
純模糊邏輯系統僅由模糊規則庫和模糊推理機組成,如圖5所示,其輸入輸出均為模糊集合。由於純模糊邏輯系統的輸入和輸出均為模糊集合,而現實世界大多數工程系統的輸入和輸出都是精確值,因此純模糊邏輯系統不能直接套用於實際工程中。為解決這一問題,有關學者在純模糊邏輯系統的基礎上提出了具有模糊產生器和模糊消除器的Mamdani型模糊邏輯系統,日本學者高木(Takagi)和關野(Sugeno)則提出了模糊規則的後項結論為精確值的模糊系統,稱為高木-關野型模糊邏輯系統。
 圖5 純模糊邏輯系統
圖5 純模糊邏輯系統高木-關野(Takagi-Sugeno)型模糊邏輯系統
高木-關野(Takagi-Sugeno)型模糊邏輯系統的結構如圖6所示,它是一類較特殊的模糊邏輯系統,其模糊規則不同於一般的模糊規則形式。高木-關野型模糊邏輯系統的輸出量在沒有模糊消除器的情況下仍然是精確值。它的優點是由於輸出量可以用輸入值的線性組合來表示,因 而 能 充 分 利 用 參 數 估 計 的 方 法 來 確 定 系 統 的 參 數,同時可以用線性控制系統的分析方法來近似分析和設計模糊邏輯系統。該系統的缺點是規則的輸出部分不具有模糊語言值的形式,因而不能充分利用專家知識,模糊邏輯的各種原則在此系統中的套用的自由度也受到限制。
 圖6 Takagi-Sugeno 型模糊邏輯系統
圖6 Takagi-Sugeno 型模糊邏輯系統Mamdani型模糊系統
在 Mamdani 型模糊系統中,模糊規則的前件和後件均為模糊語言值,它實質上是在純模糊邏輯系統的輸入和輸出部分分別添加模糊產生器和模糊消除器,其結構如圖7所示。該系統的輸入與輸出均為精確量,因而可以直接在實際工程中套用。由於其套用的廣泛性,又稱為模糊系統的標準模型。
 圖7Mamdani型模糊系統
圖7Mamdani型模糊系統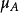
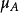
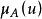
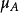
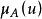
 圖1
圖1 圖2
圖2 圖3
圖3 圖4模糊系統的基本架構
圖4模糊系統的基本架構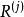
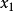
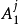

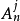
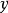
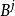
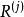
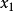
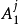

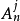

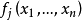
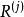
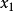
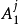

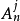

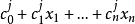
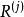
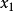
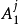

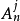


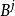
 圖5 純模糊邏輯系統
圖5 純模糊邏輯系統 圖6 Takagi-Sugeno 型模糊邏輯系統
圖6 Takagi-Sugeno 型模糊邏輯系統 圖7Mamdani型模糊系統
圖7Mamdani型模糊系統