TSK模糊系統是由Takagi、Sugeno和Kang提出的，具有很好的非線性逼近能力，被廣泛運用到系統辨識、模式識別、圖像處理和數據挖掘等多個領域。TSK模糊系統是最著名的模糊系統之一，以“IF-then”規則來定義模糊系統的規則，特別適合於用來建模。
基本介紹
- 中文名：TSK模糊系統
- 外文名：TSK fuzzy system
- 提出者：Takagi、Sugeno和Kang
- 規則：if-then
- 學科：控制科學與工程
- 優勢：良好的非線性逼近能力
基本概念,系統結構,系統優勢,
基本概念
Takagi-Sugeuo-Kang(TSK)模糊系統是由Takagi、Sugeno和Kang提出的，由於其良好的逼近性能而被廣泛運用到系統辨識、模式識別、圖像處理和數據挖掘等多個領域。模糊系統的主要問題是模糊規則的提取。常用的算法有模糊聚類法、神經網路和遺傳算法。這些算法都存在過學習問題，從而導致所設計的模糊系統缺乏良好的推廣能力。
TSK模糊系統是最著名的模糊系統之一，具有很好的非線性逼近能力，廣泛套用於智慧型學習領域，特別適合於用來建模。在TSK模糊系統中，用以“IF-then”規則來定義模糊系統的規則。
系統結構
一階TSK模糊系統的第i個模糊規則的表示形式如下:
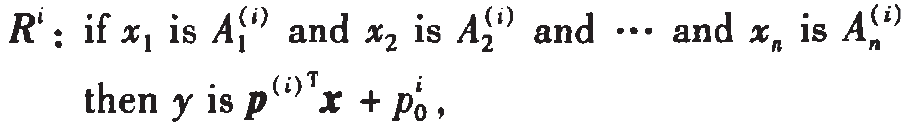
其中，
為模糊集，
，i=1,2…M；j=1,2…n。n是輸入向量的維數，M是規則個數，TSK模糊系統的實值輸出為：
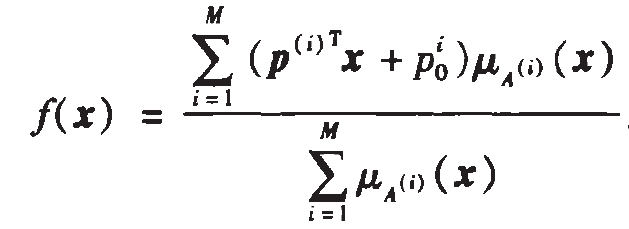
其中，
是實值輸入，
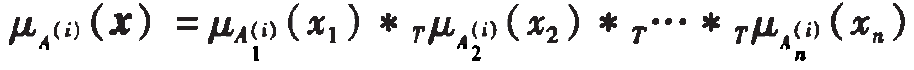
*T中T是t-norm。令
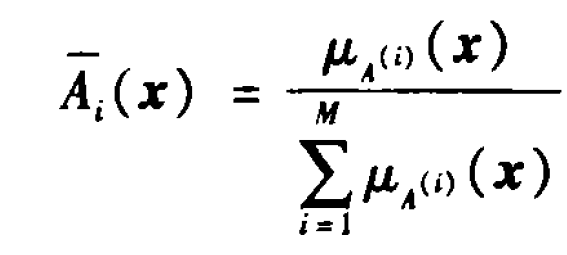
則
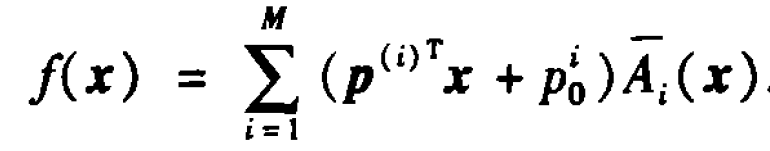
令
則
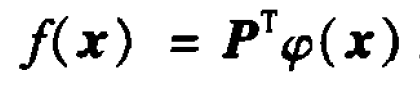
其中
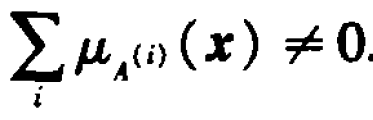
從上述公式可以看到TSK模糊系統等價於一個模糊規則空間
上的線性回歸系統。
系統優勢
TSK模糊邏輯系統由於其自身的特點在狀態預估領域有著廣泛的套用前景。首先常規的預測方法很難以滿足現場的實際要求，其原因主要有：
①未來引起的情況變化不可能事先確地全部掌握；
②即使知道某些複雜因素會對系統產生影響，但要定量地獲取和準確判斷其影響仍有困難；
③很多實際問題還有賴於預測人員的判斷能力和經驗，傳統的、沒有人工智慧技術的方法需要人工干預才能滿足實際的預測要求。
而同時TSK模糊邏輯系統是基於規則的，既可以利用誤差等數據信息，也可利用專家的經驗知識，這就為在預測系統中設計合適的修正子系統提供了靈活性；其次模糊邏輯無需建立對象的數學模型，而預測系統要建立起精確的數學模型是很困難的。最後TSK模糊邏輯系統屬於非線性系統，一般生化過程預測對象都是非線性的，要對其進行誤差反饋修正，調節器應該是非線性的，因此通過模糊系統的合理設計和調節，是可以得到理想的預測誤差修正機制。
