簡介
構想有兩個孿生兄弟甲和乙,甲乘飛船作太空旅行,乙留在地面等待甲。甲所乘坐的飛船在極短的時間內加速到速度v(速度v接近
光速c)。然後飛船以速度v作勻速直線飛行,飛船飛行很長一段時間後,迅速調頭並繼續以速度v作勻速直線飛行。回到地面時緊急減速、降落,並與一直在地面上的乙會合。
甲只在啟動、調頭、減速降落的三段時間內有
加速度,其餘的絕大部分時間都在作勻速直線飛行,處於
狹義相對論適用的
慣性系。太空飛行期間所度過的時間。則當甲作高速太空旅行,返回時會發現乙比甲變老了。 如果飛船速度非常接近
光速c,
相對論效應就會非常明顯,如若v = 0.9999c ,則T=70.71τ。即如在這一對孿生兄弟20歲時,甲乘飛船作太空飛行,甲認為飛行時間只有一年,在其返回地面時,甲只有21歲,但他卻發現乙卻成了90多歲的老人了,亦即乙比甲年老了許多。
但是,以上情形還可以換另一個角度來考察。即對於乘坐太空飛船的甲來說,甲在飛船上靜止不動,甲看到乙在極短的時間內朝相反的方向加速到速度v,然後乙以速度v作勻速直線飛行,乙飛行很長一段時間後,迅速調頭並繼續以速度v作勻速直線飛行,在與甲會合時緊急減速。在甲看來,乙只在啟動、調頭、減速的三段時間內有加速度,其餘的絕大部分時間都在作勻速直線飛行、亦處於狹義相對論適用的
慣性系。
 孿生兄弟甲和乙,甲乘飛船作太空旅行
孿生兄弟甲和乙,甲乘飛船作太空旅行因此,在甲看來,如果略去乙啟動、調頭、減速這三段時間(因這三段時間相對很短),在乙離開飛船期間,乙所度過的時間τ與甲所度過的時間T也應存在前述關係(狹義相對論一般將相對於靜止系統作勻速直線運動的系統內靜止的鐘所走過的時間記為τ,稱為該系統的原時) 這樣,在甲乙會面時,甲比乙變老了。即如乙作勻速直線飛行的速度為v = 0.9999c ,在乙飛離甲一年後與甲會面時,乙只有21歲,但他卻發現甲卻成了90多歲的老人了,亦即甲比乙年老了許多。
可見,從不同的角度分析其結論是不同的,而且是相互矛盾的。究竟是乙比甲年老了許多還是甲比乙年老了許多?還是兩者都錯了,二人應該一樣年輕?這個命題就叫做“雙生子佯謬”。
由來
1905年10月,德國《
物理年鑑》雜誌刊登了一篇《關於運動物體的電動力學》的論文,它宣告了狹義相對論假說的問世。正是這篇看似很普通的論文,建立了全新的時空觀念,並向明顯簡單的同時性觀念提出了挑戰。我們知道由
愛因斯坦狹義相對論可以得出運動的物體存在
時間膨脹效應。

在1911年4月波隆哲學大會上,法國物理學家P.
朗之萬用雙生子實驗來質疑狹義相對論的
時間膨脹效應,構想的實驗是這樣的:一對雙胞胎,一個留在地球上,另一個乘坐火箭到太空旅行。飛行速度接近
光速,在太空旅行的雙胞胎中的一人回到地球時只不過兩歲,而他的兄弟早已死去了,因為地球上已經過了200年了。
這就是著名的雙生子佯謬。
解釋
由於地球可近似為
慣性系,甲要經歷加速與減速過程,是
變加速運動參考系,真正討論起來非常複雜,因此這個
愛因斯坦早已討論清楚的問題,被許多人誤認為相對論是自相矛盾的理論。如果用
時空圖和
世界線的概念討論此問題就簡便多了,只是要用到許多數學知識和公式。
在此只是用語言來描述一種最簡單的情形。不過只用語言無法更詳細說明細節,有興趣的請參考一些相對論書籍。我們的結論是,無論在哪個參考系中,甲都比乙年輕。因為甲是經過加速的,你看剛開始在地球上,於乙的相對速度為0,而後來速度接近光速了(注意是接近)。很明顯是變速運動了,所以這樣一來就不能說是 “認為甲看乙在運動,乙看甲也在運動,為什麼不能是乙比甲年輕呢?”這句話根本就是對相對論錯誤的理解。而且甲的年輕是相對於乙的,對於他本人來說是不存在多活多少時間這么一說的。
為使問題簡化,只討論這種情形,火箭經過極短時間加速到
亞光速,飛行一段時間後,用極短時間調頭,又飛行一段時間,用極短時間減速與地球相遇。這樣處理的目的是略去加速和減速造成的影響。在地球參考系中很好討論,火箭始終是動鐘,重逢時甲比乙年輕。在火箭參考系內,地球在勻速過程中是動鐘,時間進程比火箭內慢,但最關鍵的地方是火箭掉頭的過程。
在掉頭過程中,地球由火箭後方很遠的地方經過極短的時間划過半個圓周,到達火箭的前方很遠的地方。這是一個"
超光速"過程。只是這種超光速與相對論並不矛盾,這種"超光速"並不能傳遞任何信息,不是真正意義上的超光速。如果沒有這個掉頭過程,火箭與地球就不能相遇,由於不同的參考系沒有統一的時間,因此無法比較他們的年齡,只有在他們相遇時才可以比較。
火箭掉頭後,甲不能直接接受乙的信息,因為信息傳遞需要時間。甲看到的實際過程是在掉頭過程中,地球的時間進度猛地加快了。在甲看來,乙先是比甲年輕,接著在掉頭時迅速衰老,返航時,乙又比自己衰老的慢了。重逢時,自己仍比乙年輕。也就是說,相對論不存在邏輯上的矛盾。
注意,這不是基於不同參照系的觀測效果,而是弟弟和哥哥各自度過的固有時間的差異。固有時間可以用各自在閔氏空間中
運動軌跡的四維長度除以光速得到,這個四維長度是不依賴於參照系的。
右面的只有一個空間軸𝑥的
時空圖可能對理解本題有些幫助,假定哥哥出行到達的最遠點為L,出行去程速度和回程速度都是v;。則弟弟的世界線是沿ADEC的一條直線,哥哥的世界線是折線ABC。為了繪圖方便,圖中L取成1,v=0.5 c。
令β=v/c,則B點坐標為:x =L,ct=L/β;
C點坐標為: x =0,ct=2*L/β紅色的
雙曲線的
曲線方程為:
 雙生子的時空圖
雙生子的時空圖藍色雙曲線方程為:
來計算。
因此連線A點到紅色的雙曲線上的任何一點的直線段的四維線長,都是相等的(對比
歐氏空間,歐氏空間中和一點距離相當的點,是在一個圓周上。而閔氏時空則是在兩條雙曲線上)。也就是從A點開始沿直線段走到紅色雙曲線上任意一點所花費的固有時,也就是線長除以光速都相等。
同樣的道理,藍色雙曲線上的點,沿直線段走到C點所花費的
固有時也都相等。因此有AB的固有時等於AD的固有時,BC的固有時等於EC的固有時,而線段AC比AD加上EC還要長出DE一段,所以可以知道ADEC這條路徑比ABC這條路徑耗費的固有時要長。這樣留在地球上的弟弟要比出行的哥哥度過了更長的時間,也就是說,見面時哥哥比弟弟年輕。
選用不同的
慣性系作為基準坐標系,A、B、C、D、E點,會沿
雙曲線移動,因此固有時不變,也就是說在任何參照系看,結果都是一樣的。接下來的幾幅時空圖展現了特點。左邊的圖是把哥哥去程的慣性系作為基準坐標系,右邊是把哥哥回程的慣性系作為基準坐標系。左圖中AB和右圖中BC為垂直線,說明哥哥相對基準坐標系來說是靜止的。
這兩個圖中,ADEC依然比ABC長出DE那段長度。圖中這條雙曲線與其對稱軸的交點,只是在基準坐標系中看起來有點特殊,事實上,雙曲線上的任一點,都可以找到一個基準坐標系,使得它成為這條雙曲線與其對稱軸的交點。因此雙曲線上的點都是平權的。類似的,在最初的那幅時空圖中,D、E分別是紅色雙曲線和藍色雙曲線與其對稱軸的交點,而在左圖中B成了紅色雙曲線與其對稱軸的交點,在右圖中,B成了藍色雙曲線與其對稱軸的交點。有關更複雜的情況,請參考文獻。
例子
首先讓我們來看一個例子。假設我們一家來到了俄國著名的物理學家和天文學家科學家
伽莫夫(後移居美國)筆下湯普金斯先生曾經夢遊過的城市,在這座城市裡由於速度極限(光速)很低,所以相對論效應非常顯著。來到這座城市後,我們進了一家瑞士鐘錶店,每人選了自己喜歡的一塊表並要求營業員把三塊表的時間調成一致。隨後,我們來到了一家遊樂園,其中一個遊樂項目是乘坐光速飛車,其實飛車的速度並沒有達到光速。我站在起點A處,幫兒子把安全帶系牢,兒子高興地坐在A點的光速飛車裡。我妻子站在終點B處,A與B之間的距離為L。車馬上要出發了,我下意識地對了一下自己和兒子的表,時間一分一秒都不差。抬頭再看終點處妻子的表,我發現妻子的表比我的錶慢了一些。來不及多想車已經象離弦的箭一樣沖了出去。我突然發現兒子的表越走越慢,當然是相對我的表而言,最後到達終點時與我妻子的表一致了。看來瑞士表的質量也不怎么樣,我打算玩完回去後把表給退了。在回來的路上我看了一眼妻子和兒子的表,奇怪!怎么我們的表顯示的時間分秒不差,我明明看見他們倆的表比我的慢了呀!我把我的發現告訴了我的妻子,她說她也覺得挺奇怪的,但是與我所說的現象稍有些不同。兒子在起點時,她發現我和兒子的手錶都比她的錶慢了,但當兒子乘坐飛車向她駛來時,兒子的表卻變得越來越快,最後到達終點時竟與她的表一致了。這時候兒子也加入了我們的談話,他告訴了我他的發現,他是這樣描述的,在起點處他發現爸爸的表跟他的表時間是一致的,媽媽的表走得比他的慢,當車運動起來後,爸爸的表變慢了而媽媽的表比原來快了,最後當他到達終點時媽媽的表與他的表又一致了。
從上面這個例子中,我們看到由於三個人所處的狀態不同,得出的結論也大相逕庭。但都有一個共同的特點,就是每個人都是以他本人的時間為基準作出判斷的。我們知道光速是有限的,光在空間運行是需要時間的。當所研究的對象涉及到空間大尺度範圍或當物體運動的速度大到可以與光速相提並論時,光通過空間兩點所需的時間就不能不考慮進來,這樣通常在小尺度低速度情況下被認為是同時發生的兩個事件就不能再認為是同時的了。愛因斯坦也正是從時間的
同時性入手,提出了狹義相對論。在我們生活的宇宙中,時間是非物質的量,它是為了描述物體運動而人為引進的一個物理概念。
經典物理對時間是這樣定義的“絕對的、真正的和數學的時間自身在流逝著,而且由於其本性而在均勻地,與任何其他外界事物無關地流逝著”。這一定義在研究空間小尺度範圍或低速運動的物體時,無疑是正確的,因為它暗含這樣一個概念即時間的同時性是絕對。但在研究空間大尺度範圍或高速運動的物體時,這一定義是否仍然有效,取決於對時間的同時性是如何定義的,同時還要看空間兩點兩個事件發生的時間是如何記錄的。
假設
假設有兩個完全一樣的鐘被放置在AB兩地。我們可採用中點對
鐘法將兩地的鐘校準。我們說發生在AB兩地的兩個事件是同時的,如果AB兩地的鐘所指示的時間是一樣的話。這個結論暗含有這樣一個條件即在AB兩地分別有兩個觀察者記錄本地事件發生的時間,然後再將兩個時間進行對比,判斷這兩個事件是否是同時發生的,判斷的結果與AB兩地的位置無關。從這個意義上說時間的同時性是絕對的。我們再看另一種情況,我們仍採用同樣的方法將AB兩地的鐘校準。從A點觀察AB兩地同時發生的兩個事件,得到的結論是A地的事件先於B地的事件,相差的時間與兩地之間的距離有關。同理,從B點觀察AB兩地同時發生的兩個事件,得到的結論則是B地的事件先於A地的事件。按照這個結論,時間的同時性又是相對的。所以說時間的同時性是相對的還是絕對的完全取決於時間是如何測量的。狹義相對論所涉及的是後一種情況。
1971年,美國海軍天文台把四台
銫原子鐘裝上飛機從華盛頓出發,分別向東和向西作環球飛行。結果發現,向東飛行的銫鐘與停放在該天文台的銫鐘之間讀數相差59納秒,向西飛行時,這一差值為273納秒。雖然在這次試驗中沒有扣除地球引力所造成的影響,但測量結果表明,“雙生兒佯謬”是確實存在的。
疑問?貌似根據這個實驗結論是不能證明雙生子佯謬的,這個悖論的核心表達是 A > B的同時也存在B > A。
在不懷疑實驗過程的正確性前提下,只出現了A > B 這一種情況,而沒有出現B>A的情況,也沒有解釋根據理論推導出的邏輯謬論跟實際結論之間如何修正來達到一致。
相對論認為世界線A的長度就是留在地球上的兄弟A經歷的時間,B的長度就是做星際旅行的兄弟B經歷的時間,兩條線不一樣長,也就是說,雙胞胎兄弟二人經歷了不同長度的時間。哪一個人經歷的時間長呢?有人會說直線比曲線短,那A比B經歷的時間要短啊。雙生子佯謬不是說B比A年輕嗎?怎么會反過來呢?其實,並沒有反過來,你之所以認為B線比A線長,是上了
歐氏幾何的當。我們通常用的幾何是歐氏幾何,兩點之間以線段距離為最短。但在相對論中,四維時空的幾何不是歐氏的,而是偽歐氏的。在偽歐氏幾何中,斜邊的平方等於兩條直角邊的平方差,兩點之間以直線距離為最長。所以曲線B比直線A短,B經歷的時間也就比A短。雙胞胎中的星際旅行者經歷的時間比地球上的同胞兄弟經歷的時間短。因此返航會面時,B將比A年輕。雙生子佯謬是真實的效應,它可以使太空人在有生之年到達非常遙遠的星系。
運動物體的情況又如何呢?假設有一枚火箭從A點運動到B點。火箭上裝有校對好的時鐘。我們仍採用中點對鐘法在AB兩點之間A1、A2、A3...放置一系列校對好的時鐘,並在A1、A2、A3...的每一個位置上都設有一個觀察員記錄火箭經過的時間。一切就緒火箭出發了。在A點的觀察員立刻發現火箭上的鐘變得越來越慢了,時間變慢的速度與火箭的速度有關。而據A1、A2、A3...的觀察員報告,火箭在通過他們所在的位置時,火箭上鐘的指示與本地鐘的指示是一樣的。而在B點觀察員則發現,在火箭未出發前,火箭上鐘的指示已經比B點的時間慢了一些,但隨著火箭逐漸接近,火箭上的時鐘卻變得越來越快,當到達B點時竟然與B點的時鐘是一樣的。如果在火箭里也有一個觀察員,他會得到這樣的結論即當火箭運動起來後,A點的鐘變慢了,B點的鐘變快了而沿途所經過的鐘所指示的時間與火箭上的時間是一致的。在上面的例子中,火箭相對於A和B的運動方向是不同的,所以從A點和B點觀察的結果也應是不同的,相對於A點時間是變慢了,相對於B點時間是變快了。時間是變快了還是變慢了取決於觀察者與被觀察的物體之間的距離是增加還是減少了,變快變慢的速度與兩個物體之間的相對運動速度有關。
推導
介紹
推導
時間膨脹效應時,一個方便的方法是將測量長度垂直於運動方向,從而將時間膨脹效應孤立起來,避免尺度收縮效應的干擾。推導過程可參見
張三慧《
大學物理》第二版第一冊227-230頁。
到目前為止,我們都是在基於
光速不變這樣一個前提下討論問題的。光速不變假設是愛因斯坦從
麥可遜-莫雷實驗的否定結果中得出的推論。在上面的討論中,運動物體的速度V是這樣得到的,在AB兩地分別放置兩個校準好的時鐘,AB兩地之間的距離為L。在A點記錄物體出發的時刻,在B點記錄物體到達的時刻,用兩地之間的距離L除以兩地所記錄的時間差,就得到了運動物體的速度,這樣計算的結果與兩地之間的距離無關。當然還可以用另一種方法,在A點記錄物體發出的時刻,在物體經過B點返回到A點時,記錄物體到達的時刻,用兩倍的距離L除以在A點記錄的時間差,就得到運動物體的速度。這兩種算法的結果是一樣的。如果從A點來觀察運動的物體在一去一回時速度是否是一樣呢?用我們上面所得到的時間膨脹和時間收縮效應的結論,我們可以得出,物體在離開A點後,速度是變慢的,而當物體從B點返回時,速度又是變快的,當然這是從A點觀察所得到的結果。
狹義相對論還存在另外一種效應即尺縮效應。可以採用同樣的方法,證明運動物體的長度隨觀察者與運動物體之間的距離的減少,還存在長度伸長的效應。通過以上討論,我們清楚了,同時性是相對的還是絕對的取決於觀察時間的方法,離開這一點強調同時性是相對的還是絕對的是沒有意義的。即使按照同時性是相對的觀點,時間除了膨脹效應外,還應有收縮的效應,所以說雙生子佯謬本身是不存在的。
 四維時空中的雙生子佯謬示意圖
四維時空中的雙生子佯謬示意圖證明
設S為慣性系,表示地球,S'表示飛船。在S看來,S'先加速,再以速度v勻速前進,再減速然後掉頭然後加速返回,然後以-v勻速返回,然後減速到達。加速減速的時間可以忽略不計,所以T=t/sqr(1-b^2),b=v/c。在S'看來,S開始在一個引力場中下降,直到速度為-v,然後引力場消失以-v勻速運行,然後在引力場g作用中減速到0,然後下降直到速度為v,然後
引力場消失,以v勻速運行,然後在引力場中減速直到靜止。單考慮勻速部分,t1=T1/sqr(1-b^2)。但是,在引力場中變換公式為T2=t2(1+gx/c^2)。所以只考慮從-v到v的減速加速過程。設這個過程時間為t2,則g=2v/t2,距離x等於vt1,所以T2=t2+2t1v^2/c^2=t2+2t1b^2。所以總時間T=2T1+T2=2sqr(1-b^2)t1+b^2t1+t2=t1/sqr(1-b^2)+t2。忽略t2可得T=t/sqr(1-b^2)。這裡計算的誤差為b^4或更高階。更加詳細的計算表明T>t總是成立的。以上推導來自
 孿生兄弟甲和乙,甲乘飛船作太空旅行
孿生兄弟甲和乙,甲乘飛船作太空旅行
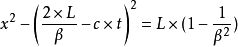

 四維時空中的雙生子佯謬示意圖
四維時空中的雙生子佯謬示意圖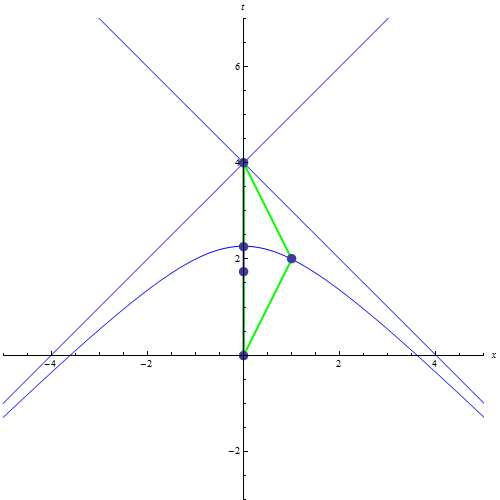
 孿生兄弟甲和乙,甲乘飛船作太空旅行
孿生兄弟甲和乙,甲乘飛船作太空旅行
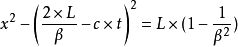

 四維時空中的雙生子佯謬示意圖
四維時空中的雙生子佯謬示意圖