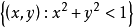簡介
凡是不涉及到
平行公理的幾何命題,在歐氏幾何中如果是正確的,在雙曲幾何中也同樣是正確的。而依賴於平行公理的命題,在雙曲幾何中都不成立。下面舉幾個例子加以說明:
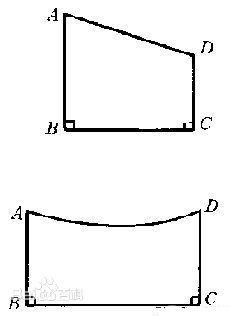 圖1.羅巴切夫斯基幾何相關圖形
圖1.羅巴切夫斯基幾何相關圖形垂直於同一直線的兩條直線平行。
存在相似而不全等的多邊形。
過不在同一直線上的三點可以做且僅能做一個圓。
雙曲幾何:
垂直於同一直線的兩條直線,當兩端延長的時候,離散到無窮。不存在相似而不全等的多邊形。
過不在同一直線上的三點,不一定能做一個圓。
從上面所列舉得羅巴切夫斯基幾何的一些命題可以看到,這些命題和我們所習慣的直觀有矛盾。所以羅巴切夫斯基幾何中的一些幾何事實沒有象歐氏幾何那樣容易被接受。但是,我們可以用習慣的歐氏幾何中的事實作一個直觀“模型”來解釋羅氏幾何是正確的。
模型
羅巴切夫斯基幾何的公理系統有幾種直觀的模型。羅巴切夫斯基幾何中的非定義概念(元名)在各種模型中被定義為具體的對象,使得雙曲幾何的公理被這種模型滿足。
龐加萊模型
Poincare model:在雙曲幾何的龐加萊模型中,“點”是龐加萊圓盤
(即平面上單位圓盤的內部)上的點,“直線”是所有包含在龐加萊圓盤內,並於單位圓垂直相交的圓弧。在這個模型內,可以證明過兩“點”有唯一的“直線”等雙曲幾何的公理。而且我們可以看到,過“直線”外的一點有不止一條“直線”和已知“直線”平行(即不相交)。
克萊因模型
Klein model:在克萊因模型中,“點”仍然是龐加萊圓盤上的點,“直線”是單位圓的所有弦(chord)。這個模型仍然滿足雙曲幾何的所有公理。但克萊因模型中兩條直線的夾角並不等於歐氏幾何意義下的夾角。
辨析
平行線
平行線是公理幾何中非常重要的概念。如果兩條直線沒有交點,那么它們稱為平行。在歐氏幾何中,平行線的性質本質上由平行公理刻畫。它等價於如下陳述:“過直線外一點有且只有一條直線和已知直線平行”。而在羅巴切夫斯基幾何中,平行線變多了。從“過直線外一點至少有兩條不同的直線和已知直線平行”,我們可以證明過這一點有無窮多條平行線。
三角形
歐氏幾何中三角形的內角和是180度。這個命題依賴於歐氏幾何的平行公理。而在雙曲幾何中,任何三角形的內角和一定是嚴格小於180度;內角和與180度的差稱為這個三角形的“缺陷”(defect)。這個數值與三角形的面積成正比例。而因為缺陷最多是180度,所以在雙曲幾何中,三角形的面積不可能無限大。這又是與歐氏幾何的直覺完全相反的現象。
發展歷程
1893年,在
喀山大學樹立起了世界上第一個為數學家雕塑的塑像。這位數學家就是俄國的偉大學者、非歐幾何的重要創始人——
羅巴切夫斯基(Никола́й Ива́нович Лобаче́вский, Nikolai Ivanovich Lobachevskii, 尼古拉·伊萬諾維奇·羅巴切夫斯基)。
非歐幾何是人類認識史上一個富有創造性的偉大成果,它的創立,不僅帶來了近百年來數學的巨大進步,而且對
現代物理學、天文學以及人類時空觀念的變革都產生了深遠的影響。
不過,這一重要的數學發現羅巴切夫斯基提出後相當長的一段時間內,不但沒能贏得社會的承認和讚美,反而遭到種種歪曲、非難和攻擊,使非歐幾何這一新理論遲遲得不到學術界的公認。
羅巴切夫斯基是在嘗試解決歐氏
第五公設問題的過程中,從失敗走上他的發現之路的。歐氏第五公設問題是
數學史上最古老的著名難題之一,它是由古希臘學者最先提出來的。
公元前三世紀,希臘亞歷山大里亞學派的創始者歐幾里得集前人幾何研究之大成,編寫了
數學發展史上具有極其深遠影響的數學巨著《幾何原本》。
這部著作的重要意義在於,它是用公理法建立科學理論體系的最早典範。在這部著作中,歐幾里得為推演出幾何學的所有命題,一開頭就給出了五個公理(適用於所有科學)和五個
公設(只套用於幾何學),作為邏輯推演的前提。《幾何原本》的注釋者和評述者們對五個公理和前四個公設都是很滿意,唯獨對第五個公設(即
平行公理)提出了質疑。
第五公設是論及
平行線的,它說的是:如果一直線和兩直線相交,且所構成的兩個同側內角之和小於兩直角,那么,把這兩直線延長,它們一定在那兩內角的一側相交。數學家們並不懷疑這個
命題的真實性,而是認為它無論在語句的長度,還是在內容上都不大像是個
公設,而倒像是個可以證明的定理,只是由於歐幾里得沒能找到它的證明,才不得不把它放在公設之列。
為了給出第五公設的證明,完成歐幾里得沒能完成的工作,自公元前3世紀起到19世紀初,數學家們投入了無窮無盡的精力,他們幾乎嘗試了各種可能的方法,但都遭到了失敗。
羅巴切夫斯基是從1815年著手研究
平行線理論的。開始他也是循著前人的思路,試圖給出第五公設的證明。在保存下來的他的學生聽課筆記中,就記有他在1816~1817學年度在幾何教學中給出的一些證明。可是,很快他便意識到自己的證明是錯誤的。
前人和自己的失敗從反面啟迪了他,使他大膽思索問題的相反提法:可能根本就不存在第五
公設的證明。於是,他便調轉思路,著手尋求第五公設不可證的解答。這是一個全新的,也是與傳統思路完全相反的探索途徑。羅巴切夫斯基正是沿著這個途徑,在試證第五公設不可證的過程中發現了一個嶄新的幾何世界。
羅巴切夫斯基創造性地運用了處理複雜數學問題常用的一種邏輯方法——
反證法。這種反證法的基本思想是,為證“第五公設不可證”,首先對第五公設加以否定,然後用這個否定命題和其它
公理公設組成新的公理系統,並由此展開邏輯推演。
首先假設第五
公設是可證的,即第五公設可由其它公理公設推演出來。那么,在新公理系統的推演過程中一定會出現邏輯矛盾,至少第五公設和它的否定命題就是一對邏輯矛盾;反之,如果在“第五公設不可證”的新公理系統的推演中不出矛盾,就反駁了“第五公設可證”這一假設,從而也就間接證得“第五公設不可證”。
依照這個邏輯思路,羅巴切夫斯基對第五公設的等價命題——普列菲爾
公理“過平面上直線外一點,只能引一條直線與已知直線不相交”作以否定,得到否定命題“過平面上直線外一點,至少可引兩條直線與已知直線不相交”,並用這個否定命題和其它公理公設組成新的公理系統展開邏輯推演。
在推演過程中,他得到一連串古怪、非常不合乎常理的命題。但是,經過仔細審查,卻沒有發現它們之間存在任何邏輯矛盾。於是,遠見卓識的羅巴切夫斯基大膽斷言,這個“在結果中並不存在任何矛盾”的新公理系統可構成一種新的幾何,它的邏輯完整性和嚴密性可以和
歐幾里得幾何相媲美。而這個無矛盾的新幾何的存在,就是對第五
公設可證性的反駁,也就是對第五公設不可證性的邏輯證明。由於尚未找到新幾何在現實界的原型和類比物,羅巴切夫斯基慎重地把這個新幾何稱之為“想像幾何”。
1826年2月23日,羅巴切夫斯基於喀山大學物理數學系學術會議上,宣讀了他的第一篇關於非歐幾何的論文:《幾何學原理及平行線定理嚴格證明的摘要》。這篇論文的問世,標誌著非歐幾何的誕生。然而,這一重大成果剛一公諸於世,就遭到正統數學家的冷漠和反對。
參加2月23日學術公議的全是數學造詣較深的專家,其中有著名的數學家、天文學家西蒙諾夫,有後來成為科學院院士的古普費爾,以及後來在數學界頗有聲望的博拉斯曼。在這些人的心目中,羅巴切夫斯基是一位很有才華的青年數學家。可是,出乎他們的意料,這位年輕的教授在簡短的開場白之後,接著說的全是一些令人莫名其妙的話,諸如三角形的內角和小於兩直角,而且隨著邊長增大而無限變小,直至趨於零;銳角一邊的垂線可以和另一邊不相交,等等。這些命題不僅離奇古怪,與
歐幾里得幾何z相衝突,而且還與人們的日常經驗相背離。然而,報告者卻認真地、充滿信心地指出,它們屬於一種邏輯嚴謹的新幾何,和歐幾里得幾何有著同等的存在權利。這些古怪的語言,竟然出自一個頭腦清楚、治學嚴謹的數學家教授之口,不能不使與會者們感到意外。他們先是表現現一種疑惑和驚呆,不多一會兒,便流露出各種否定的表情。
宣講論文後,羅巴切夫斯基誠懇地請與會者討論,提出修改意見。可是,誰也不肯作任何公開評論,會場上一片冷漠。一個具有獨創性的重大發現作出了,那些最先聆聽到發現者本人講述發現內容的同行專家,卻因思想上的守舊,不僅沒能理解這一發現的重要意義,反而採取了冷談和輕慢的態度,這實在是一件令人遺憾的事情。
會後,系學術委員會委託西蒙諾夫、古普費爾和博拉斯曼組成三人鑑定小組,對羅巴切夫斯基的論文作出書面鑑定。他們的態度無疑是否定的,但又遲遲不肯寫出書面意見,以致最後連文稿也給弄丟了。
羅巴切夫斯基的論文沒能引起學術界的注意和重視,論文本身也似石沉大海,不知被遺棄何處。但他並沒有因此灰心喪氣,而是頑強地繼續獨自探索新幾何的奧秘。1829年,他又撰寫出一篇題為《幾何學原理》的論文。這篇論文重現了第一篇論文的基本思想,並且有所補充和發展。此時,羅巴切夫斯基已被推選為喀山大學校長,可能出自對校長的“尊敬”,《喀山大學通報》全文發表了這篇論文。
1832年,根據羅巴切夫斯基的請求,喀山大學學術委員會把這篇論文呈送彼得堡科學院審評。科學院委託著名數學家奧斯特羅格拉茨基院士作評定。奧斯特羅格拉茨基是新推選的院士,曾在
數學物理、
數學分析、力學和
天體力學等方面有過卓越的成就,在當時學術界有很高的聲望。可惜的是,就是這樣一位傑出的數學家,也沒能理解羅巴切夫斯基的新幾何思想,甚至比喀山大學的教授們更加保守。
如果說喀山大學的教授們對羅巴切夫斯基本人還是很“寬容”的話,那么,奧斯特羅格拉茨基則使用極其挖苦的語言,對羅巴切夫斯基作了公開的指責和攻擊。同年11月7日,他在給科學院的鑑定書中一開頭就以嘲弄的口吻寫道:“看來,作者旨在寫出一部使人不能理解的著作。他已經達到了自己的目的。”接著,對羅巴切夫斯基的新幾何思想進行了歪曲和貶低。最後粗暴地斷言:“由此我得出結論,羅巴切夫斯基校長的這部著作謬誤連篇,因而不值得科學院的注意。”
這篇論文不僅引起了學術界的惱怒,而且還激起了社會上反動勢力的敵對叫囂。名叫布拉切克和捷列內的兩個人,以匿名在《祖國之子》雜誌上撰文,公開指名對羅巴切夫斯基進行人身攻擊。
針對這篇污辱性的匿名文章,羅巴切夫斯基撰寫了一篇反駁文章。但《祖國之子》雜誌卻以維護雜誌聲譽為由,將羅巴切夫斯基的文章扣壓下來,一直不予發表。對此,羅巴切夫斯基極為氣憤。
羅巴切夫斯基開創了數學的一個新領域,但他的創造性工作在生前始終沒能得到學術界的重視和承認。就在他去世的前兩年,俄國著名數學家布尼雅可夫斯基還在其所著的《平行線》一書中對羅巴切夫斯基發難,他試圖通過論述非歐幾何與經驗認識的不一致性,來否定非歐幾何的真實性。
英國著名數學家莫爾甘對非歐幾何的抗拒心裡表現得就更加明顯了,他甚至在沒有親自研讀非歐幾何著作的情況下就武斷地說:“我認為,任何時候也不會存在與
歐幾里得幾何本質上不同的另外一種幾何。”莫爾甘的話代表了當時學術界對非歐幾何的普遍態度。
在創立和發展非歐幾何的艱難歷程上,羅巴切夫斯基始終沒能遇到他的公開支持者,就連非歐幾何的另一位發現者德國的高斯也不肯公開支持他的工作。
高斯是當時數學界首屈一指的數學巨匠,負有“歐洲數學之王”的盛名,早在1792年,也就是羅巴切夫斯基誕生的那一年,他就已經產生了非歐幾何思想萌芽,到了1817年已達成熟程度。他把這種新幾何最初稱之為“反歐幾何”,後稱“星空幾何”,最後稱“非歐幾何”。但是,高斯由於害怕新幾何會激起學術界的不滿和社會的反對,會由此影響他的尊嚴和榮譽,生前一直沒敢把自己的這一重大發現公之於世,只是謹慎地把部分成果寫在日記和與朋友的往來書信中。
當高斯看到羅巴切夫斯基的德文非歐幾何著作《平行線理論的幾何研究》後,內心是矛盾的,他一方面私下在朋友面前高度稱讚羅巴切夫斯基是“俄國最卓越的數學家之一”,並下決心學習俄語,以便直接閱讀羅巴切夫斯基的全部非歐幾何著作;另一方面,卻又不準朋友向外界泄露他對非歐幾何的有關告白,也從不以任何形式對羅巴切夫斯基的非歐幾何研究工作加以公開評論;他積極推選羅巴切夫斯基為哥廷根皇家科學院通訊院士,可是,在評選會和他親筆寫給羅巴切夫斯基的推選通知書中,對羅巴切夫斯基在數學上的最卓越貢獻--創立非歐幾何卻避而不談。
高斯憑任在數學界的聲望和影響,完全有可能減少羅巴切夫斯基的壓力,促進學術界對非歐幾何的公認。然而,在頑固的保守勢力面前他卻喪失了鬥爭的勇氣。高斯的沉默和軟弱表現,不僅嚴重限制了他在非歐幾何研究上所能達到的高度,而且客觀上也助長了保守勢力對羅巴切夫斯基的攻擊。
晚年的羅巴切夫斯基心情更加沉重,他不僅在學術上受到壓制,而且在工作上還受到限制。按照當時俄國大學委員會的條例,教授任職的最高期限是30年,依照這個條例,1846年羅巴切夫斯基向人民教育部提出呈文,請求免去他在數學教研室的工作,並推薦讓位給他的學生波波夫。
人民教育部早就對不順從他們意志辦事的羅巴切夫斯基抱有成見,但又找不到合適的機會免去他在喀山大學的校長職務。羅巴切夫斯基辭去教授職務的申請正好被他們用以作為藉口,不僅免去了他主持教研室的工作,而且還違背他本人的意願,免去了他在喀山大學的所有職務。被迫離開終生熱愛的大學工作,使羅巴切夫斯基在精神上遭到嚴重打擊。他對人民教育部的這項無理決定,表示了極大的憤慨。
家庭的不幸格外增加了他的苦惱。他最喜歡的、很有才華的大兒子因患肺結核醫治無效死去,這使他十分傷感。他的身體也變得越來越多病,眼睛逐漸失明,最後終於什麼也看不見了。
1856年2月12日,偉大的學者羅巴切夫斯基在苦悶和抑鬱中走完了他生命的最後一段路程。喀山大學師生為他舉行了隆重的追悼會。在追悼會上,他的許多同事和學生高度讚揚他在建設喀山大學、提高民族教育水平和培養數學人材等方面的卓越功績,可是誰也不提他的非歐幾何研究工作,因為此時,人們還普遍認為非歐幾何純屬“無稽之談”。
羅巴切夫斯基為非歐幾何的生存和發展奮鬥了三十多年,他從來沒有動搖過對新幾何遠大前途的堅定信念。為了擴大非歐幾何的影響,爭取早日取得學術界的承認,除了用俄文外,他還用法文、德文發行了自己的著作,同時還精心設計了檢驗大尺度空間幾何特性的天文觀測方案。
不僅如此,他還發展了非歐幾何的解析和微分部分,使之成為一個完整的、有系統的理論體系。在身患重病,臥床不起的困境下,他也沒停止對非歐幾何的研究。他的最後一部巨著《論幾何學》,就是在他雙目失明,臨去世的前一年,口授他的學生完成的。
歷史是最公允的,因為它終將會對各種思想、觀點和見解作出正確的評價。1868年,義大利數學家
貝特拉米發表了一篇著名論文《非歐幾何解釋的嘗試》,證明非歐幾何可以在歐氏空間的曲面上實現。這就是說,非歐幾何命題可以“翻譯”成相應的歐氏幾何命題,如果歐氏幾何沒有矛盾,非歐幾何也就自然沒有矛盾。
直到這時,長期無人問津的非歐幾何才開始獲得學術界的普遍注意和深入研究,羅巴切夫斯基的獨創性研究也由此得到學術界的高度評價和一致讚美,這時的羅巴切夫斯基則被人們讚譽為“幾何學中的哥白尼”。
 圖1.羅巴切夫斯基幾何相關圖形
圖1.羅巴切夫斯基幾何相關圖形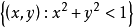

 圖1.羅巴切夫斯基幾何相關圖形
圖1.羅巴切夫斯基幾何相關圖形