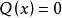抽象的講,一個n維雙曲空間就是一個高斯曲率處處為常數的流形。在腦海中形成雙曲空間這種圖形的概念非常困難,數學家認為這種形狀擁有負常曲率(constant negative curvature),而球形擁有正常曲率(constant positive curve)。
基本介紹
- 中文名:雙曲空間
- 外文名:Hyperbolic space
- 套用學科:數學
- 術語類別:幾何
簡介,雙曲平面,
簡介
在n維實射影空間Pn中,取射影坐標,考慮Pn內的二次曲面
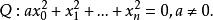
設使Q變為自身的Pn的射影變換的全體所構成的群為G,稱Q為絕對形(absolute),G稱為契約變換群(congruent transformation group)。
當a<0時,Q是實二次曲面。設Q的內點的全體為Hn,則群G對於Hn的作用是可遷的。體系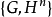 是雙曲幾何,Hn稱為n維雙曲空間。Hn的點稱為尋常點(ordinary point ),Q上的點稱為無窮遠點(point at infinity ),Q的外部的點稱為超無窮遠點(ultra infinite point)。所謂Hn的兩條直線平行,意味著它們在絕對形上相交。
是雙曲幾何,Hn稱為n維雙曲空間。Hn的點稱為尋常點(ordinary point ),Q上的點稱為無窮遠點(point at infinity ),Q的外部的點稱為超無窮遠點(ultra infinite point)。所謂Hn的兩條直線平行,意味著它們在絕對形上相交。
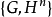
當a>0時,Q是虛二次曲面,群G對於Pn的作用是可遷的。體系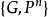 是橢圓幾何學中,同一平面上的不同的兩條直線必交於一點。將非歐幾何作上述表示時,稱該表示為克萊因模型(Klein's model)。
是橢圓幾何學中,同一平面上的不同的兩條直線必交於一點。將非歐幾何作上述表示時,稱該表示為克萊因模型(Klein's model)。
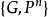
雙曲平面
[hyperbolic plane]
域上非奇異的、維數為2的迷向二次空間稱作雙曲平面,即域上的2維向量空間,帶有一個二次型Q,且存在非零向量x ,使得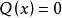 ,雙曲平面的名稱來源於二次型Q與2維歐幾里得空間中雙曲線方程的相似性。特徵不為2的域上的任意兩個雙曲平面都是等距的。有限維雙曲平面的正交直和稱為雙曲空間。
,雙曲平面的名稱來源於二次型Q與2維歐幾里得空間中雙曲線方程的相似性。特徵不為2的域上的任意兩個雙曲平面都是等距的。有限維雙曲平面的正交直和稱為雙曲空間。