基本介紹
釋義
 隨機遊走
隨機遊走定律介紹
無規則行走
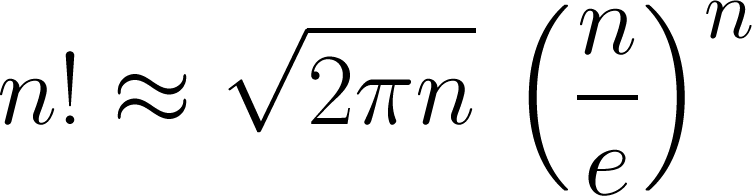 斯特林公式
斯特林公式 醉酒人的無規則行走
醉酒人的無規則行走
隨機漫步理論一般指本詞條
 隨機遊走
隨機遊走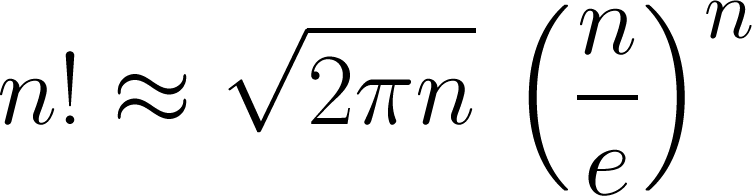 斯特林公式
斯特林公式 醉酒人的無規則行走
醉酒人的無規則行走隨機遊走(random walk)也稱隨機漫步,隨機行走等是指基於過去的表現,無法預測將來的發展步驟和方向。核心概念是指任何無規則行走者所帶的守恆量都各自對應著一個擴散運輸定律,接近於布朗運動,是布朗運動理想的數學狀態,現階段主要套用...
隨機漫步理論(Random Walk Theory)1959年,奧斯本(M.F.M Osborne)提出了隨機漫步理論,認為股票交易中買方與賣方同樣聰明機智,股票價格的形成,取決於市場對隨機到來的事件信息作出的實際反應,現今的股價已基本反映了供求關係。股票...
本書也是行為金融理論的入門讀本,作者綜述了各種有關行為金融的概念及作家,如黑天鵝、漫步華爾街、希勒、量子物理原理、施萊弗的非有效市場,股票個股的隨機性與市場的系統性,有助於我們從實證的角度更加深入地理解了市場屬性,如何從新的...
當前,有關金融資產定價和股票市場波動的代表性理論,主要有如下幾種:凱恩斯選美論、隨機漫步理論(Random Walk Theory)、現代資產組合理論(MPT)、有效市場假說(EMH)、行為金融學(BF)等。金融投資理論 凱恩斯選美論 選美論是由英國...
1959年,奧斯本(M.F.M Osborne)提出了隨機漫步理論,認為股票交易中買方與賣方同樣聰明機智,現今的股價已基本反映了供求關係;股票價格的變化類似於化學中的分子“布朗運動”,具有隨機漫步的特點,其變動路徑沒有任何規律可循。因此,股價波動...
隨機漫步理論(Random Walk Theory)1959年,奧斯本(M.F.M Osborne)提出了隨機漫步理論,認為股票交易中買方與賣方同樣聰明機智,現今的股價已基本反映了供求關係;股票價格的變化類似於化學中的分子“布朗運動”,具有隨機漫步的特點,其...
有代表性的股票投資理論包括:隨機漫步理論、現代資產組合理論、有效市場假說、行為金融學、演化證券學等。專家理論 人類對於股市運行邏輯與規律的認知,是一個極具挑戰性的世界級難題。迄今為止,尚沒有任何一種理論和方法能夠令人信服並且...
隨機漫步理論(Random Walk Theory)1959年,奧斯本(M.F.M Osborne)提出了隨機漫步理論,認為股票交易中買方與賣方同樣聰明機智,現今的股價已基本反映了供求關係;股票價格的變化類似於化學中的分子“布朗運動”,具有隨機漫步的特點,其...
隨機漫步理論(Random Walk Theory)1959年,奧斯本(M.F.M Osborne)提出了隨機漫步理論,認為股票交易中買方與賣方同樣聰明機智,現今的股價已基本反映了供求關係;股票價格的變化類似於化學中的分子“布朗運動”,具有隨機漫步的特點,其...
隨機漫步理論(Random Walk Theory)1959年,奧斯本(M.F.M Osborne)提出了隨機漫步理論,認為股票交易中買方與賣方同樣聰明機智,現今的股價已基本反映了供求關係;股票價格的變化類似於化學中的分子“布朗運動”,具有隨機漫步的特點,其...
《股市十大理論》將股票市場內最有用的10個理論,以簡潔文筆寫出這10個理論包括: 一、道氏理論 二、隨機漫步理論 三、周期理論 四、李本博士民眾論 五、尾市理論 六、相反理論 七、亞當理論 八、江恩理論 九、波浪理論 十、集中...
反射理論不適用於常態的近似均衡。只要把從認知與現實之間的暫時背離加以忽略,有效市場理論所主張的隨機漫步理論就可以充分發揮作用。反射理論可以用於對衝擊基金的巨觀投資戰略。在金融市場上,大多數投資工具的價格波動範圍(圍繞均值)為一...
隨機漫步 1964年奧斯本提出了“隨機漫步理論”,他認為股票價格的變化類似於化學中的分子“布朗運動”(懸浮在液體或氣體中的微粒所做的永不休止的、無秩序的運動),具有“隨機漫步”的特點,也就是說,它變動的路徑是不可預期的。1970年...
證券研究者已經在這方面做了許多有益的探索,這包括趨勢理論、波浪理論、江恩理論,市場行為心理學理論、遺傳理論,全息理論、隨機漫步理論、混沌理論等。這些理論或是基於觀察的經驗總結,或是理論套用的嘗試,各有所長,各有不足。那么,有沒...
第6章 技術分析與隨機漫步理論 6.1 鞋上有破洞、股市預測朦朧難解 6.2 股市存在趨勢嗎 6.3 究竟何為隨機漫步 6.4 一些更為精細複雜的技術分析方法 6.5 其他幾個幫你賠錢的技術理論 6.6 技術分析大師 6.7 為何技術分析師仍...
第6章 技術分析與隨機漫步理論 / 115 鞋上有破洞,預測中有朦朧 / 116 股市存在趨勢嗎 / 117 究竟何為隨機漫步 / 119 一些更為精細複雜的技術分析方法 / 122 其他幾個幫你賠錢的技術理論 / 128 為何技術分析師仍能安居樂業 /...
第七章 技術分析與隨機漫步理論 鞋子上的破洞和預言的朦朧 股市有“慣性”嗎 隨機漫步的真實面目 一些更為精細的技術體系 “過濾器”體系 道氏理論 相對強弱體系 量價體系 讀取圖形 難以接受的隨機性 一組幫助你賠錢的技術理論 “裙擺...
當前,有關金融資產定價和股票市場波動邏輯的代表性理論,主要有如下幾種:凱恩斯選美論、隨機漫步理論(Random Walk Theory)、現代資產組合理論(MPT)、有效市場假說(EMH)、行為金融學(BF)等。凱恩斯選美論 選美論是由英國著名經濟學家...
隨機漫步理論(Random Walk Theory)隨機漫步理論認為股票交易中買方與賣方同樣聰明機智,股票價格的形成,取決於市場對隨機到來的事件信息作出的實際反應,現今的股價已基本反映了供求關係。股票價格的變化類似於“布朗運動”,具有隨機漫步的...
隨機漫步理論(Random Walk Theory)1959年,奧斯本(M.F.M Osborne)提出了隨機漫步理論,認為股票交易中買方與賣方同樣聰明機智,現今的股價已基本反映了供求關係;股票價格的變化類似於化學中的分子“布朗運動”,具有隨機漫步的特點,其...
隨機漫步理論(Random Walk Theory)1959年,奧斯本(M.F.M Osborne)提出了隨機漫步理論,認為股票交易中買方與賣方同樣聰明機智,現今的股價已基本反映了供求關係;股票價格的變化類似於化學中的分子“布朗運動”,具有隨機漫步的特點,其...
認知的不完備性直接造成了參入者的種種偏向,所以有效市場學說、隨機漫步理論等等皆是空談。股票市場的技術分析理論是建立在市場永遠有效這一前提下,所謂市場反應一切,以前發生過的事情以後也會重複等等。但技術分析有天然的缺陷,只是...
隨機漫步理論(Random Walk Theory)1959年,奧斯本(M.F.M Osborne)提出了隨機漫步理論,認為股票交易中買方與賣方同樣聰明機智,現今的股價已基本反映了供求關係;股票價格的變化類似於化學中的分子“布朗運動”,具有隨機漫步的特點,其...
投資定律16:華爾街隨機漫步理論 投資定律17:市場是有效的 投資定律18:不要聽窮人的投資建議 投資定律19:完美的投資組合永遠也不需要交易 投資定律20:賬面虧損並非實際虧損 投資定律21:市盈率對股票有效但對股市無效 投資定律22:沒...
貝納理論 第五章長期浪和當前的複合體 第六章股票和商品 個股 商品 黃金 第七章股票市場分析的其他方法及其與波浪理論的關係 道氏理論 “康德拉蒂耶夫波”的經濟循環 循環 十年的模式 訊息 隨機漫步理論 技術分析 “經濟分析”手段 ...
隨機漫步理論 1959年,奧斯本(M.F.M Osborne)提出了隨機漫步理論,認為股票交易中買方與賣方同樣聰明機智,現今的股價已基本反映了供求關係;股票價格的變化類似於化學中的分子“布朗運動”,具有隨機漫步的特點,其變動路徑沒有任何規律...
