間接平差是在確定多個未知量的最或然值時,選擇它們之間不存在任何條件關係的獨立量作為未知量組成用未知量表達測量的函式關係、列出誤差方程式,按最小二乘法原理求得未知量的最或然值的平差方法。間接平差為平差計算最常用的方法,其數學模型比較簡單,便於評定平差值及其函式的精度。
基本介紹
- 中文名:間接平差
- 外文名:Indirect Adjustment
- 適用學科:誤差理論與測量平差基礎
定義
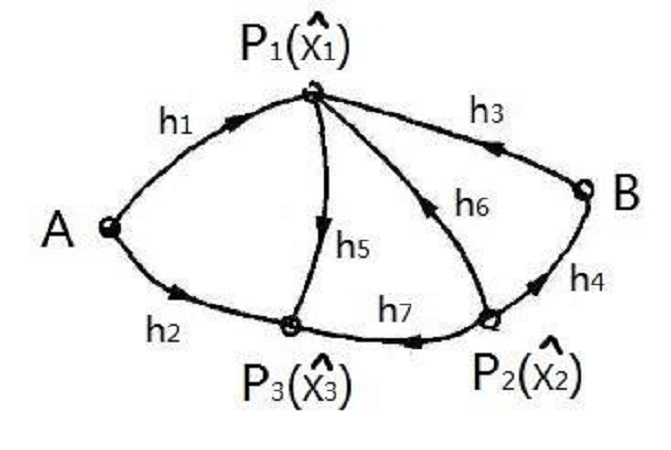
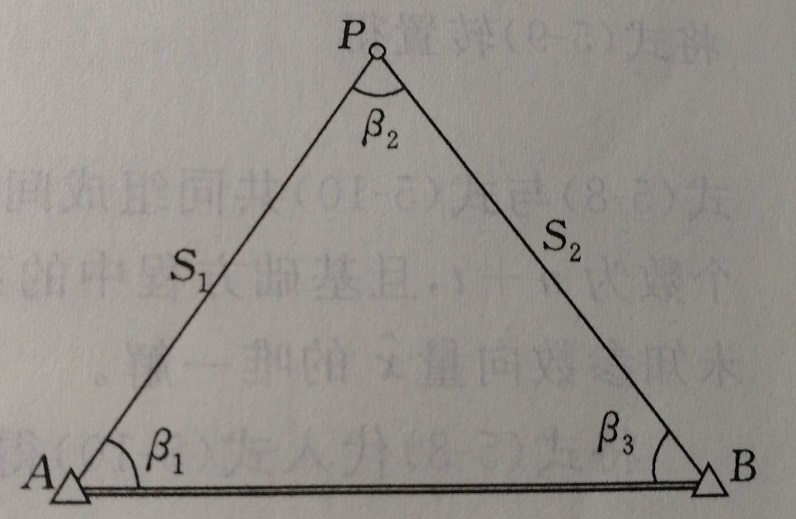 圖1 邊角網
圖1 邊角網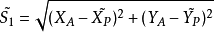
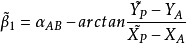
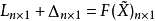
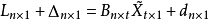
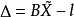
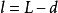
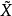
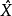
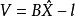
原理
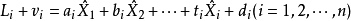
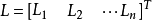
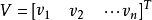
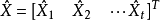
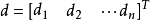
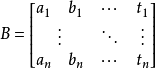
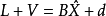
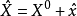
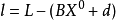
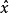
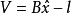
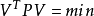
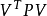
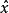
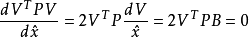
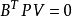
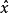
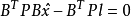
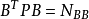
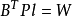
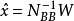
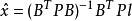
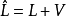
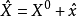
過程與步驟
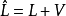
間接平差是在確定多個未知量的最或然值時,選擇它們之間不存在任何條件關係的獨立量作為未知量組成用未知量表達測量的函式關係、列出誤差方程式,按最小二乘法原理求得未知量的最或然值的平差方法。間接平差為平差計算最常用的方法,其數學模型比較簡單,便於評定平差值及其函式的精度。
 圖1 邊角網
圖1 邊角網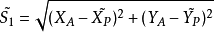
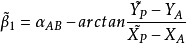
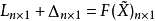
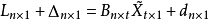
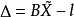
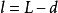
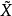
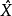
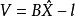
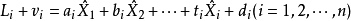
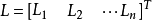
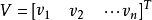
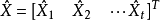
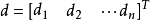
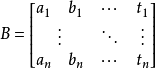
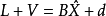
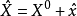
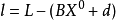
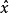
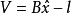
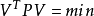
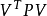
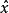
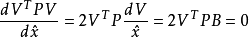
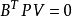
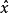
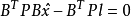
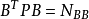
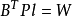
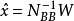
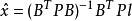
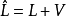
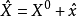
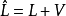
間接平差是在確定多個未知量的最或然值時,選擇它們之間不存在任何條件關係的獨立量作為未知量組成用未知量表達測量的函式關係、列出誤差方程式,按最小二乘法原理求...
條件平差的前提是有多餘觀測量, 條件方程式的個數與多餘觀測量有關,每有一個多餘觀測量,就可列出一個獨立的條件方程式,在進行條件平差時,應列出與多餘觀測數...
在測量控制網當中,同一個未知點通過不同的線路推算得到的坐標觀測值會有所不同,全部觀測值的加權平均值就叫做這個點坐標平差值。...
“結點平差”一般是用來檢查拓撲的,比如兩條線段(道路)在交叉口應該接上的,但是由於某種原因沒接上,你可以使用自動節點平差,設定一下檢查容限,讓計算機自動接上...
測量平差是德國數學家高斯於1821~1823年在漢諾瓦弧度測量的三角網平差中首次套用,以後經過許多科學家的不斷完善,得到發展,測量平差已成為測繪學中很重要的、內容...
測量平差法是用最小二乘法原理處理各種觀測結果的理論和計算方法。測量平差法的目的在於消除各觀測值間的矛盾,以求得最可靠的結果和評定測量結果的精度。任何測量...
測量平差是德國數學家高斯於1821~1823年在漢諾瓦弧度測量的三角網平差中首次套用,以後經過許多科學家的不斷完善,得到發展,測量平差已成為測繪學中很重要的、內容...
《測量平差基礎》是2007年測繪出版社出版的圖書,作者是武漢測繪科技大學測量平差教研室。全書共分11章,可作為測繪基礎課教材,及有關專業工程技術人員學習參考。...
邊角網是監測網最常用的形式,網中既測角又測邊可以提高縱橫向點位精度。邊角網常用間接平差法。...
《誤差理論與測量平差》是2010年1月1日同濟大學出版社出版的圖書。本書是測繪和地理信息系統及相關專業誤差理論與測量平差基礎課程的教材。...
《測量平差-第二版》是2013年2月中國礦業大學出版社出版的圖書,作者是張書畢。...... 第四章介紹間接平差的原理和方法,第五章介紹各種平差方法的實際套用,第六...
測量平差”既是測繪學科重要的專業基礎課,同時又是一門套用科學,是多個套用領域數據處理的基礎。...
出版信息測量平差實訓指導 作者: 譚立萍 黃富勇 編輯:趙斌 頁數:115頁 開本:16 版次:1次 日期:2016年8月 裝幀:簡裝 ISBN:9787518916375內容簡介測量平差是高職...
本書是在高等學校測繪學科教學指導委員會的指導下,以全國高等學校測繪學科教學指導委員會"十五"高職高專規劃教材研討會上制定的《測量平差》教學大綱為主要依據,在...
《測量平差(修訂版)》是1994年地質出版社出版的圖書。...... 平差;兩組平差;間接平差;誤差橢圓;導線網平差;測邊網、邊角網平差;高程控制網平差。...
本習題集是高職工程測量技術等測繪類專業測量平差課程必備的配套教學參考書。全書共分為8章36節,約170題,涵蓋了測量的基本誤差理論和平差方法,內容全面,針對性...
滿秩平差是指配置足夠的起始數據,根據最小二乘法原理利用矩陣進行測量平差的方法。...... 滿秩平差的特點是:測量控制網進行間接觀測平差時,由於有足夠的起始數據...
《高等教育"十二五"規劃教材:測量平差(第2版)》共分八章,第一章介紹測量誤差及其傳播定律,第二章介紹平差數學模型與最小二乘原理,第三章介紹條件平差的原理和...
《測量平差基礎通用習題集》是1999年武漢測繪科技大學出版社出版的圖書,作者是高士純...
附有未知數的條件平差(condition adjustmentwith unknowns)平差計算中的基本方法之一它類似於條件平差法.不同之處是:平差時除了觀測量之外,還選定u個獨立的非觀...
《控制網平差程式設計》是2004年原子能出版社出版的圖書,作者是郭九訓。...... 第三章 控制網平差程式設計的主要方法3.1 平差方法的選擇3.2 附有條件的間接觀...
《誤差理論與測量平差基礎習題集》是2005年武漢大學出版社出版的圖書,作者是武漢大學測繪學院測量平差學科組。...
為了克服以上問題,並且充分利用水準網平差中的信息,將間接平差函式模型轉化為條件平差函式模型,利用條件方程式中的所有信息,搜尋出獨立閉合環或附合路線並快速解算...
張琦等人對附合的1條水準路線圖解平差方法研究發現,該方法作業步驟簡單,且能夠滿足三、四等水準測量的精度要求。王磊等人通過對間接平差模型的簡化,利用Matlab編制了...
其原始觀測數據經過儀器格值係數改正、周期誤差改正、潮汐改正、氣壓改正、儀器高改正等預處理以後得到測點間的觀測段差,將段差作為平差元素,採用間接平差模型,即可...
海洋測繪 2006, 26(4): 21–23.[12] 牛貴蘭, 張書畢. 多元回歸分析的間接平差算法[J]. 鐵道勘察, 2006, 1: 22–24.[13] 王劍, 張書畢. 變形預測的...
多餘觀測是測量平差計算中的一個術語。它是指在一組觀測值中,除了能惟一確定某個幾何或物理模型的t個必要觀測之外的其餘觀測值。多餘觀測即觀測值的個數多於確定...
