基本介紹
- 中文名：時間膨脹
- 外文名：time dilation
- 別名：鐘慢效應
- 適用學科：狹義相對論
- 定義：物理現象
簡介,定義,實驗證明,速度時間膨脹實驗,引力時間膨脹實驗,速度和引力時間膨脹結合實驗,介子衰期,太空飛行與時間膨脹,參見,
簡介
時間膨脹是一種物理現象：兩個完全相同的時鐘之中，拿著甲鐘的人會發現乙鐘比自己的走得慢。這現象常被說為是對方的鐘“慢了下來”，但這種描述只會在觀測者的參考系上才是正確的。任何本地的時間（也就是位於同一個坐標繫上的觀測者所測量出的時間）都以同一個速度前進。時間膨脹效應適用於任何解釋時間速度變化的過程。 在阿爾伯特·愛因斯坦的相對論中，時間膨脹出現於兩種狀況：
狹義相對論中，時間膨脹效應是相互性的：從任一個時鐘觀測，都是對方的時鐘走慢了（當然我們假定兩者相互的運動的等速均勻的，兩者在觀測對方時都沒有加速度）。
相反，引力時間膨脹卻不是相互性的：塔頂的觀測者覺得地面的時鐘走慢了，而地面的觀測者覺得塔頂的時鐘走快了。引力時間膨脹效應對於每個觀測者都是一樣的，膨脹與引力場的強弱與觀察者所處的位置都有關係。
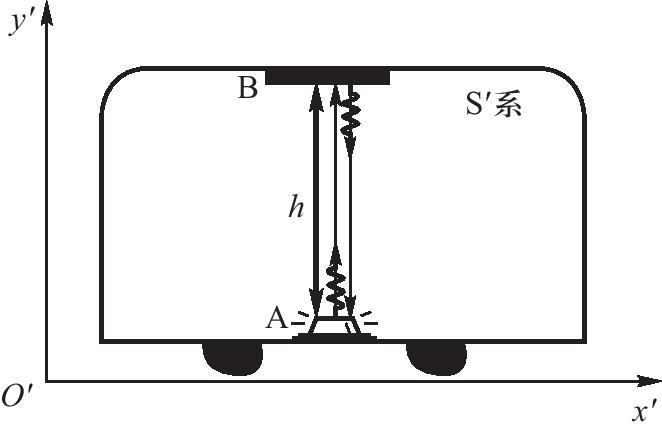
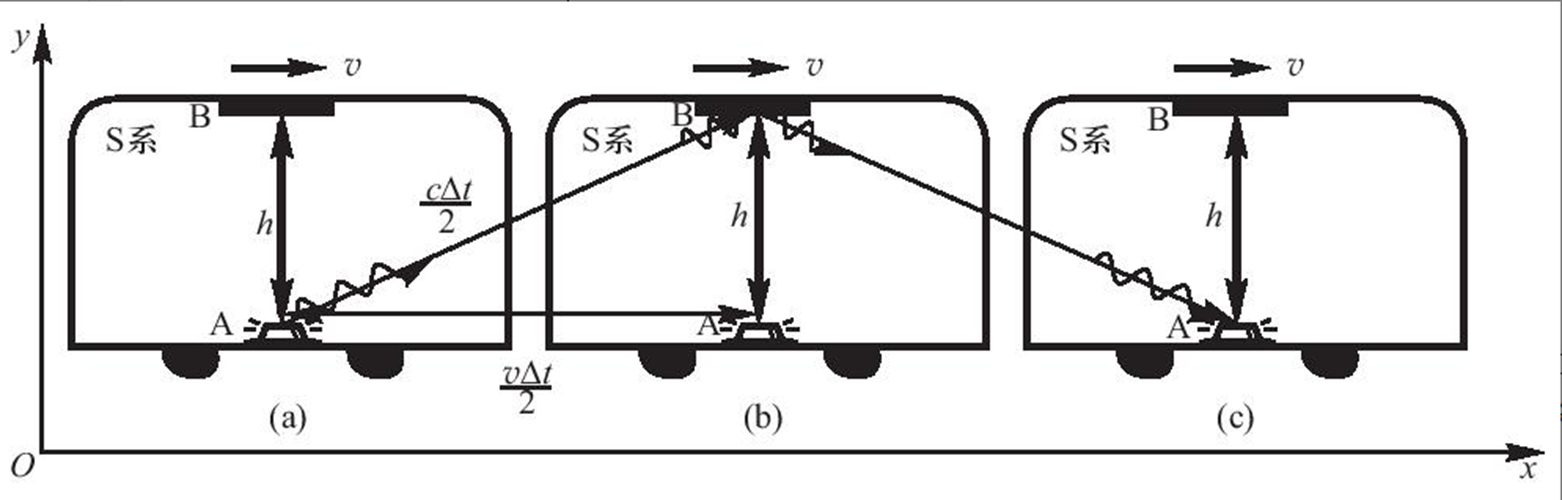
在大學物理教學過程中，講到時間膨脹效應時，通常選用如圖1所示的例子。假設有 一個高度為ｈ的火車車廂，相對於地面以速度ｖ水平向右做勻速直線運動，在火車車廂的Ａ點處有一光源豎直向上發出一束光，光束經車頂 Ｂ 處的反射鏡反射到Ａ點的接收器。將 Ａ點處發光作為事件1，A點的接收器接收到光作為事件2． 在地面上建立S參照系，在火車上建立S'參照系。在S'系中兩個事件的時間間隔是同一地點A測量的,為本徵時間 Δt’，且有 Δt'=2hc。圖2（a）為A開始發光時，（b）為反射鏡剛接收到光並反射時，（ｃ）為Ａ處接收到光時各點的位置示意圖。從 Ａ 處發光到 Ｂ 接收到光，再到 Ａ 處接收到光， 兩個事件在地面上看是在不同地點測量的．兩事件的事件間隔記為 Δt。Δt 為運動時間且滿足幾何關係 (cΔt/2)＝ (ｖΔt/2)+h。即為時間膨脹效應公式
圖1 反射鏡豎直放置時火車參照系中的事件示意圖
圖2 反射鏡豎直放置時地面參照系中的事件示意圖
定義
狹義相對論中測定時間膨脹的公式為：
當中
v是第二個時鐘相對第一個時鐘移動的速度；
c是光速；
那么移動中的那個時鐘走得就比較慢。日常生活中，就算是高速的航天飛行，造成的時間膨脹效應也太小，一般很難被探測到，因此可被忽略。只有在物體達到30,000km/s（光速的1/10）以上時，時間膨脹才顯得十分重要。
因為洛倫茲因子而引起的時間膨脹現象是於1897年由Joseph Larmor發現──最起碼有電子在原子核運轉而引起的現象。
實驗證明
速度時間膨脹實驗
- Rossi and Hall（1941）比較了位於山頂和位於海平面的由宇宙射線製造出的μ子數量。儘管μ子從山頂到地面所需的時間已經是幾個半衰期，但是在海面的μ子數量卻只是少了一點。這是由於μ子相對於測試者以高速運動，導致了可觀的時間膨脹效應。經計算，快速移動的μ子的衰變速度比它們相對測試者靜止時的衰變速度要慢10倍。
引力時間膨脹實驗
- Pound, Rebka在1959年測量出位於較低海拔（所受重力較強）的光波的頻率有很小的引力紅移。得出的數值和廣義相對論預測的數值有小於10%的偏差。不久後Pound和Snider在1964年得出更準的1%偏差，正好就是引力時間膨脹預測的效應。
速度和引力時間膨脹結合實驗
- 全球定位系統可被視為一項持續進行的狹義和廣義相對論實驗。軌道上的時鐘根據時間膨脹效應被調校成適當的速度，以對應位於地面的時鐘。另外，有關廣義相對論的一些微調已經編寫進定位衛星，要不然，每12個小時定位結果便會有大約7米的偏差。
介子衰期
比較不同速度下μ-介子的衰期是可行的。慢速的介子可在實驗室里製造，而快速的介子則在宇宙射線穿入大氣層時製造出來。實驗室中靜止介子的衰期為2.22 μs，由宇宙射線製造出來的介子的速度為光速的98%，衰期為比靜止時大5倍左右，和理論相符合。實驗中的“時鐘”是介子的衰期，而高速運動介子的時鐘有著自己的前進速度，也就是比實驗室里的“時鐘”慢許多。
太空飛行與時間膨脹
根據時間膨脹效應，太空人在相對於地球上的觀察者以極高速運動的飛船內時，對於地球觀察者而言，儘管地球已經經歷了很長的歲月，飛船內的人卻沒什麼老化，因為極大的速度會使飛船（和裡面的所有物體）的時間減慢。也就是說，地球上的觀察者會發現，當飛船的時鐘走了一圈時，地球上的時鐘已經轉了許多圈了。只要速度夠高，這個效應便會明顯地顯示出來。比方說，對地球上的觀察者而言，可能都過了十個鐘頭了，太空旅行者的手錶卻只走了一個小時。此效應對飛船或地球這兩個坐標系是對稱的，因為地球看飛船在動，飛船看地球也在動，而且速度大小相等。也就是說，對太空人而言，地球的時間才是較慢的，可能飛船的時鐘過了十分鐘，太空人卻發現地球上的時鐘只過了一分鐘(詳見更下面的段落以及孿生子佯謬)。
人們更加有可能利用這個效應把人類送到距離地球最近的恆星附近，而不需耗掉航天員的一生光陰(儘管地球上的觀察者可能會發現旅行所花的時間仍然大得誇張，但對飛船上的人而言，卻只花了更少的一段時間)。然而，要實現這種省時的情況，則需要研發一些更新、更先進的推進技術。另一個問題是，在這么高的速度下，空間裡的粒子會折射，成為高能量的宇宙射線。要想飛船不被毀滅，必須用到一些不可思議的防輻射措施。其中一種建議的措施是利用強電磁場把前來的物質離子化，或把它們反彈出去。
目前的航天科技有著許多根本性的限制，如要把飛船加速到接近光速需要大量能量，小型碎片等會對飛船造成威脅。不過，在今天的航天任務中，時間膨脹並不是考慮的因素之一，因為飛船速度相對於光速實在是太小了。另外一個太空飛行會涉及到的時間膨脹效應情況，是接近一個有著極大引力的地方，如黑洞，那裡會有強大的引力時間膨脹效應，電影星際穿越中便有相關的橋段出現。
