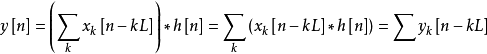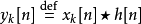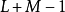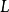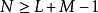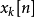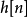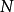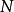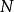重疊-相加之卷積法 ( Overlap-add method ) 是一種區塊卷積 ( block convolution, sectioned convolution ),可以有效的計算一個很長的信號 x[n] 和一個 FIR 濾波器 h[n] 的離散卷積。
基本介紹
- 中文名:重疊-相加之卷積法
- 外文名:Overlap–add method
- 分組:數理科學
形式
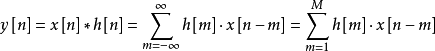
算法
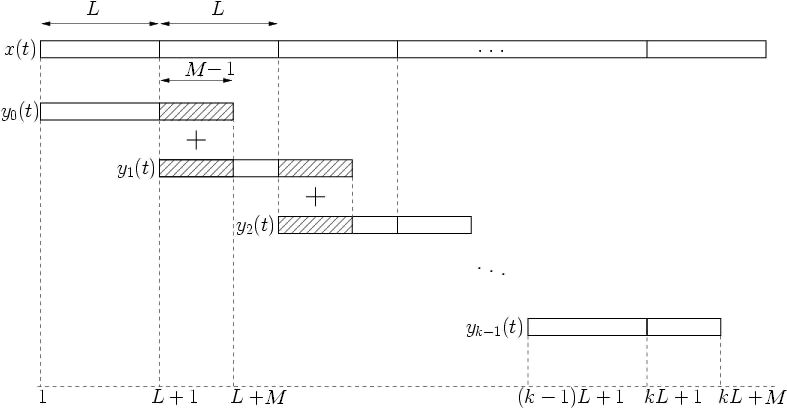

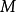
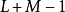
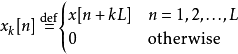
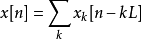
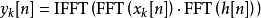
偽代碼
Algorithm (OA for linear convolution) Evaluate the best value of N and L H = FFT(h,N) (zero-padded FFT) i = 1 while i <= Nx il = min(i+L-1,Nx) yt = IFFT( FFT(x(i:il),N) * H, N) k = min(i+N-1,Nx) y(i:k) = y(i:k) + yt (add the overlapped output blocks) i = i+L end