重疊-存儲之卷積法

重疊-存儲之卷積法 ( Overlap-save method, Overlap-discard method ) 是一種區塊卷積 ( block convolution, sectioned convolution )，可以有效的計算一個很長的信號 x[n] 和一個 FIR 濾波器 h[n] 的離散卷積。

基本介紹

• 中文名：重疊-存儲之卷積法
• 外文名：Overlap-save method
• 分類：數位訊號處理、數值分析

定義

定義信號 x[n] 和一個 FIR 濾波器 h[n] 的離散卷積：

其中h[m] 在 [1,M] 之外為零。與重疊-相加之卷積法不同之處在於，重疊-存儲之卷積法所算出的輸出區塊並不重疊 (因此計算上少了將輸出區塊相加所需的加法)，而是每次用的輸入區塊有所重疊。因此實現時每次讀取輸入後需將和下一個輸入重疊的部分存儲起來，作為下一輸入區塊的開頭部分，因此稱為重疊-存儲之卷積法。另外重疊-存儲之卷積法也不需補零。

算法

概念上，這個做法是選用一個較短的適當長度 L 來切割 y[n] ，則因為 h[n] 是有限長度，因此在某一區塊內的 y[n] 也只被有限長的 x[n] 區塊（會比 y[n] 分區成的區塊長一點）所決定。因此只要選擇有影響的輸入區塊和 h[n] 卷積，再選擇結果中適當的部分即可得到正確的輸出區塊。

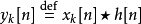
則對於在 內的n， 輸出y[n] 可寫成

所以只需計算n在 中的y_k[n+M-kL] ，亦即n在 的y_k[n] 部分即可。因此每一段輸出區塊y_k[n] 的前M-1 點可丟棄（discard）。

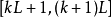
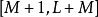
儘管一時看不出切割成區塊的好處為何，但將xk[n] 做 的周期延伸，

則 和 這兩個卷積在 的部分相等。所以可以將線性卷積改以 點循環卷積計算，結果的 部分作為輸出 y[n] 在 的部分。由於每段x_k[n] 原本就有 長，所以選擇 的話輸入 x[n] 就不需補零。 改以循環卷積計算後即可藉循環卷積定理。

變換成三次 點快速傅立葉變換和 次乘法，使原本每段 的運算量減少至 O(N logN)，速度大幅增加。

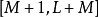
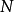
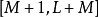
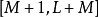
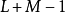
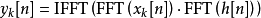
準代碼

   (Overlap-save algorithm for linear convolution)   //////// revised by fantastic ////////   N = length(x), M = length(h)   O = M – 1;    // overlap length must be M-1   L = M;    // >=1 is OK   P = O + L;   H = FFT(h, P);    // just calc once   idx = - (O - 1);    // starting index which is offset M-1 in matlab   while (idx <= N)       i1 = max(1, idx);    // must be >= 1       i2 = min(N, idx+P-1);    // must be <= N       yt = IFFT( FFT(x(i1:i2), P).*H, P );       y(idx:idx+P-M) = yt(M:P);    // discard first M-1 values and concatenate the remaining       idx = idx + L;   end   y = y(1:M+N-1);    // the first M+N-1 values are the convolution result

區塊長度的選擇

當 x[n] 的長度 N' 和 h[n] 的長度 M 相差太大時（例如 M < log2N' ），直接卷積（不透過循環卷積和 FFT ）反而最快。而當 N' 和 M 差不多在同一個數量級時，不用分區，也就是只有一塊長度 L = N' 的區塊去做FFT 即可。而當 N' 比 M 大了不少，卻沒大太多時，區塊長度 L 就需要選擇。除了與 N' 和 M 相關以外，也要考慮當兩者相除有餘數時，剩下一小段的輸入可能會造成浪費。

相關條目

• 離散卷積
  
• 循環卷積
  
• 快速傅立葉變換
  
• 重疊-相加之卷積法