兩個函式的循環卷積是由他們的周期延伸所來定義的。周期延伸意思是把原本的函式平移某個周期 T 的整數倍後再全部加起來，所產生的新函式。
基本介紹
- 中文名：圓周折積
- 外文名：Circular convolution
簡介,相關條目,
簡介
兩個函式的循環卷積是由他們的周期延伸所來定義的。周期延伸意思是把原本的函式平移某個周期T的整數倍後再全部加起來，所產生的新函式。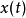
的周期延伸可以寫成
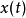
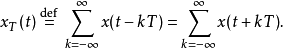
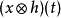
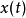
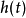
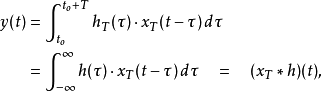
類似地，對於離散信號（數列），可以定義周期N的循環卷積{\displaystyle (x\otimes h)[n]}為
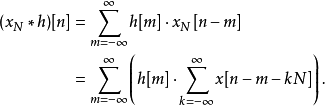
離散信號的循環卷積可以經由循環卷積定理使用快速傅立葉變換（FFT）而有效率的計算。因此，若原本的（線性）卷積能變換成循環卷積來計算，會遠比直接計算更快速。考慮到長度L和長度M的有限長度離散信號，做卷積之後會成為長度 L+M-1的信號，因此只要把兩離散信號補上適當數目的零（zero-padding）成為N點信號，其中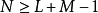 
，則它們的循環卷積就與卷積相等。即可接著用N點 FFT 作計算。
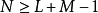
用以上方法計算卷積時，若兩個信號長度相差很多，則較短者須補上相當多的零，太不經濟。而且在某些情況下，例如較短的h[n] 是一個FIR 濾波器而較長的x[n]是未知長度的輸入（像語音）時，直接用以上方法要等所有的輸入都收到後才能開始算輸出信號，太不方便。這時可以把x[n]分割成許多適當長度的區塊（稱為 block convolution），然後一段一段的處理。經過濾波後的段落再仔細的連線起來，藉由輸入或輸出的重疊來處理區塊連線的部分。這兩種做法分別稱為重疊-儲存之卷積法和重疊-相加之卷積法。
相關條目
- 循環卷積定理
- DFT與循環卷積
