循環卷積(circular convolution) 不同於線性卷積的一種卷積運算,是周期卷積的一種。
基本介紹
- 中文名:循環卷積
- 外文名:circular convolution
- 套用學科:通信
- 領域:信息科學
定義
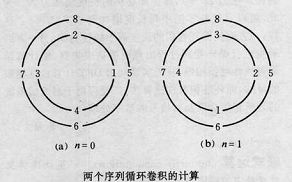 圖1
圖1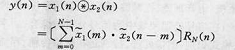 圖2
圖2 圖3
圖3線性卷積
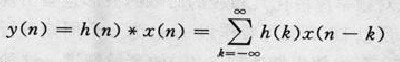 圖4
圖4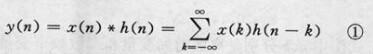 圖5
圖5循環卷積和線性卷積的關係
 圖6 循環卷積分析
圖6 循環卷積分析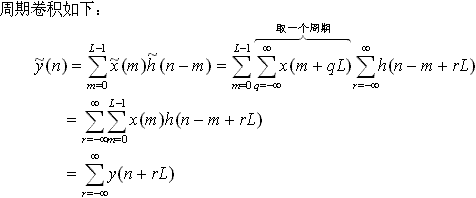 圖7 周期卷積分析
圖7 周期卷積分析 圖8 兩種卷積對比
圖8 兩種卷積對比
循環卷積(circular convolution) 不同於線性卷積的一種卷積運算,是周期卷積的一種。
 圖1
圖1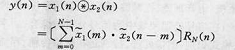 圖2
圖2 圖3
圖3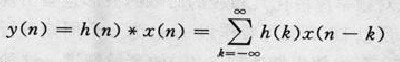 圖4
圖4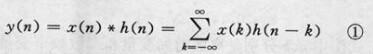 圖5
圖5 圖6 循環卷積分析
圖6 循環卷積分析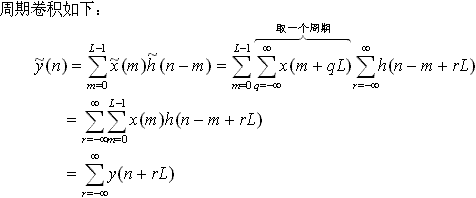 圖7 周期卷積分析
圖7 周期卷積分析 圖8 兩種卷積對比
圖8 兩種卷積對比循環卷積(circular convolution) 不同於線性卷積的一種卷積運算,是周期卷積的一種。...
循環卷積離散傅立葉變換(discrete Fouriertransform of circular convolution)一種數字變換方法.設循環卷積x3(n) = x}(n)娜二:(n ),則有 ...
離散傅氏變換循環卷積(discrete Fouriertransform circular convolution)是一種數學運算方法。...
線上性代數中,循環矩陣是一種特殊形式的 Toeplitz矩陣,它的行向量的每個元素都是前一個行向量各元素依次右移一個位置得到的結果。由於可以用離散傅立葉變換快速解...
重疊-存儲之卷積法 ( Overlap-save method, Overlap-discard method ) 是一種區塊卷積 ( block convolution, sectioned convolution ),可以有效的計算一個很長的...
重疊-相加之卷積法 ( Overlap-add method ) 是一種區塊卷積 ( block convolution, sectioned convolution ),可以有效的計算一個很長的信號 x[n] 和一個 FIR ...
線性卷積(linear convolution) 在時域描述線性系統輸入和輸出之間關係的一種運算。這種運算線上性系統分析和信號處理中套用很多,通常簡稱卷積。中文名:數位訊號處理...
3.5 有限長序列的循環卷積定理和循環相關定理3.5.1 有限長序列的循環卷積3.5.2循環卷積定理3.5.3有限長序列的線性卷積和循環卷積3.5.4線性相關與循環相關...
圓周摺積也作圓周卷積,是不同於線性卷積的一種卷積運算,周期卷積的一種。兩個函式的圓周卷積是由他們的周期延伸所來定義的。周期延伸意思是把原本的函式平移某個...
數論變換由於快速傅立葉變換的提出,大大減少了計算運算次數,乘法與加法次數是由原來的 ( )減為 (),可見大大節省計算量。在有循環卷積特性的條件下,快速數論變換...
。計算a與b的積模 ,即是計算兩個長度為K的數列的負循環卷積。為了讓負循環卷積可以正確完成,需要選取一個數字n,在模 的環中計算卷積。這就需要卷積後的各位結...
