定義
按數論,一個集合或數系Z
M={0,1,…,M-1},對其元素作加法或乘法運算時,若其結果仍屬於集合中的某一元索,則該數系定義為數環或稱Z
M,它是以M為模的整數環。當M為素數(一個大於1的整數,只能被1和它本身整除,如3,5,7,11等)則稱Z
M為數域。數論變換就是定義在整數的有限環和有限域內具有和DFT相似的結構形式。對一個有限長度N的整數序列x(n),其數論變換定義為t圖1.
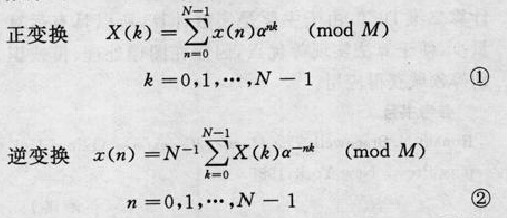 圖1
圖1式中x(n),X(k)包含在有限集合的整數環ZM里,即x(n),X(k)∈ZM,ZM={0,1,…,M…1},α是與模M(mod M)有關的參數,所以式①、②是以M為模的同餘運算。設給定一個固定的正整數M,把它叫做模,如果用M去除任意兩個整數a與b,所得餘數相同,則稱 a和b對模M同餘,並記作a=b(mod M)或b=a(mod M)。如 2≡5(mod 3),5≡8(mod 3)則 2≡8(mod 3)。所以整數a和b對模M同餘的充分必要條件是M能整除(a-b)。它等價a=b+Mq,q為整數。對一個固定的b值,有無窮多個a值與b值對模M同餘。例如,如果知道某月的2日是星期日,則9,16,23,30都是星期日,因為它們對模7都是同餘,即9≡2(mod 7),16≡2 (mod 7),……,同餘運算有一定的規則。由於DFT是在複數域上具有循環卷積特性(CCP)的唯一變換形式,而NTT是在整數域上具有CCP的變換形式,因此對式①、②只要恰當地選取參數N.M和α,就可通過NTT在整數環上進行循環卷積運算。一般變換長度N的選擇最好是2的冪或高度複合數(一個正整數除了能被1和它本身整除外,還能被另外的正整數整除),以便採用快速傅立葉變換(FFT)的各種快速算法。α的選擇可直接取2或2的冪,這樣與α相乘的運算就可以簡化為移位操作了。模M的選擇常用的有默森(Mersenne)數Mp=2-1(p為素數)和費瑪(Fermat)數Ft=2+1(b=2,t=1,2,3,…)。所以有默森數變換(MNT)和費瑪數變換(FNT)。前者無快速算法,後者有快速算法。分析表明,利用FNT的快速算法計算N點循環卷積只需作2Nlog2N次移位操作和2Nlog2N次加法,對於N≤256,比FFT提高速度約3~5倍,而且由於所有運算為取模的同餘運算,因此求得的值無捨入誤差。這些優點使NTT的硬體易於實現,但由於數論變換不具有通常譜的物理含義,因而僅適用於計算快速卷積,同時FNT變換長度N還與字長b成正比,使得長度N的增加受到一定限制。
計算方法
在快速傅立葉變換(FFT)中,變換因子是一個複數,因而需要進行複數運算。但是,,這表明WN是1的N次根。對於任意整數k,是按k對N取模呈現周期性。在數論變換中,是以整數a代替複數WN實現正變換和反變換,要求這個整數是1的N次根。這一要求在一般的整數運算規則中不成立,只有採用同餘式的運算規則才能找到滿足這一要求的a和N。利用這樣的a和N可以構成數論變換公式。
顯然,這種變換在計算速度上比快速傅立葉變換快。
把一個給定的正整數M稱為模(mod),如果用M去除任意兩個整數α和β,所得餘數相同,便稱作α和β對模M同餘,記作
α余β(modM) (2)
因此,同餘式運算規則是以正整數M為模的整數環(域上所定義的一種線性正交變換。
在式(1)中,整數a、N、M三者之間必須滿足如下關係:
aN呏1(modM) (3)
滿足上式的最小正整數N叫做a對模M的指數,a是1的N次根,或簡稱a是N階的。例如,a為2時對模7的指數是3,對模11的指數是10。
在數論變換中要求找到合適的a、N和M值。所選擇的N應當是高複合數。但如採用2的乘方,就能構成像FFT算法那樣的信號流圖,並且希望選取的N值足夠大,以滿足實際需要。其次,所選取的a應當能用簡便的方法實現乘法運算,因為在計算機中乘法運算最花費時間;如果a是2的乘方,可以用移位操作實現a的乘方運算,因而比較方便。又由於是模運算,所以不存在捨入誤差。此外,M最好也是位數不太多的二進制數,而且必須是大於2的素數。
梅森數論變換 在數論變換的一般公式 (1)中的模M採用梅森數時,就稱為梅森數論變換。麥森數為
M=2k-1 (4)
它是一奇數。令k=PQ,P為素數,便有在此情況下,最大可能的變換長度決定於(2P-1)。以(2P-1)為模,可以找到
① a=2,N=P,aN=2P呏1【mod(2P-1)】,但P是素數,N=P也是素數,不是高複合數。
② a=-2,N=2P,(-2)呏1【mod(2P-1)】,但由於N=2P,故不是高的複合數。因此,取梅森數作模是不合適的。
費馬數論變換 在數論變換中比較合理的模M是選用費馬數,即
Ft=2b+1 b=2t (5)
前幾個Ft的值是F0=3;F1=5;F2=17;F3=257;F4=65537;這五個費馬數都是素數,而F5和F6都是複合數:
F5=4294967297=641×6700417
F6=274177×67280421310721在t>4的情況下,還沒有發現一個費馬數是素數。Ft稱為第t個費馬數,模Ft的計算可用b位算術運算來完成。信號所占用的位數和濾波器係數決定了在輸出中不引起溢出誤差所需用的b值,實際用的b值比信號所占用位數的兩倍稍大。為了能夠採用費馬數,如果以溢出條件得到的b值不是一個2的冪時,應該把它增加到接近的2的冪數。
因為是按模M=Ft費馬數進行算術運算,所以長為N=2m的序數的費馬數論變換及其反變換表達式可寫成其中N是滿足此式的最小正整數。
費馬數論變換和傅立葉變換相類似。當N=2m時,數論變換的快速計算法的信號流圖和 FFT的算法信號流圖也是一致的,只是把WN換成a。但是,費馬數論變換的基本函式是由2的方冪構成,不需要使用乘法,僅為移位操作,其運算速度快於 FFT算法。加上費馬數論變換算法是模算術運算,不存在捨入誤差,從而能得到高精度的褶積。此外,由於FFT的基本函式是三角函式,需要預先存儲這些基本函式,而費馬數論變換算法卻不需要存儲基本函式。費馬數論變換的缺點主要是它沒有物理意義,在信號處理中不能運用中間過程;運算需要的字長與變換點數之間存在著嚴格的關係,隨著輸入序列的增長往往需要很長的字長。
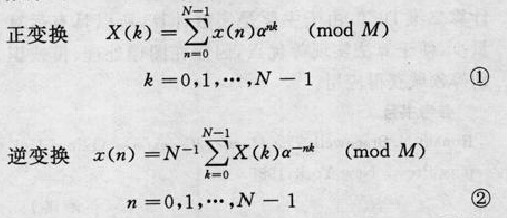 圖1
圖1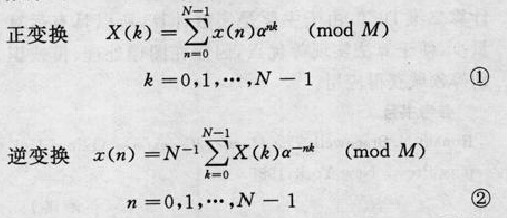 圖1
圖1