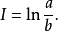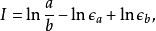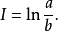基本介紹
- 中文名：重正規化
- 外文名：Renormalization
- 領域：量子力學
正規化,重正規化,相關條目,
正規化
物理學中，尤其是量子場論，正規化(regularization)是一項處理無限大、發散以及一些不合理表示式的方法，其方法透過引入一項輔助性的概念——正規子(regulator)。舉例來說，若短距離物理效應出現發散，則設定一項空間中最小距離
來解決這情形。正確的物理結果是讓正規子消失(此例是
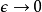)的極限情形，不過正規子的用意就在於當它是有限值，理論結果也是有限值的。正規化是將數學中的發散級數的可和性方法(summability methods)用在物理學問題上。
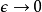
然而，理論結果通常包含了一些項，是正比於例如
的式子，若取極限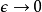
則會沒有良好定義。正規化是獲得一個完整、有限且有意義的結果的第一步；在量子場論，通常會接著一個相關但是獨立的技術方法稱作重正規化。重正規化則是基於對一些有著類似
表示式的物理量的要求，要求其應該等於觀測值。如此的約束條件則允許我們計算一些看似發散的物理量的有限值。
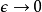
正規化的特定例子有：
- 維度正規化(Dimensional regularization)；
- 泡立-維拉斯正規化(Pauli-Villars regularization)；
- 晶格正規化(Lattice regularization)；
- ζ函式正規化(Zeta function regularization)；
- 哈達瑪正規化(Hadamard regularization)；
- 點分裂正規化(Point-splitting regularization)。
重正規化
在量子場論發展的早期，人們發現許多圈圖（即微擾展開的高階項）的計算結果含有發散（即無窮大）項。重正規化是解決這個困難的一個方案。一個理論如果只有有限種發散項，則可以在拉氏量中引進有限數目的項來抵消這些無窮大項，這種情形被稱為可重整。反之，如果理論中有無限種發散項，則稱為不可重整。
現代場論的觀點認為所有理論都只是有效理論，它們都有它們的適用範圍。除了所謂的終極理論，所有理論在原則上都是不可重整的。在這種觀點下，重正規化只是聯繫不同能標下理論的一種方法。
例如：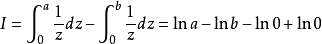
的後兩項發散。
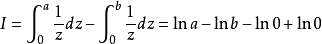
為了消除發散，把積分下限分別改為無窮小的
和
，這樣積分就變成了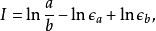
如果能保證
那么就可以得到
