簡介
量子電動力學將電磁場量子化,建立起來的方程能說明電磁波是由光子組成的,且能說明光子的產生和湮沒,亦能說明電子的波粒二象性及其產生和湮沒。為了得到更精確的理論結果,進行微擾展開高階圈圖近似計算時,由於包含自由動量的圈積分,結果不可避免地出現無窮大,使得理論計算無從與實驗相對比,稱為發散困難。經過多年研究,認識到這些無窮大結果的物理效應表現在電子的質量和電荷上。電子的質量來源於電子固有的力學質量和電子自能貢獻的電磁質量;電子的電荷來源於電子固有的電荷和由於真空極化作用所產生的附加電荷。電子自能貢獻的電磁質量及真空極化作用產生的附加電荷均為無窮大。重正化方法就是用實驗測得的電子質量和電子電荷代替電子的無窮大質量和無窮大電荷,高次近似計算中的無窮大便被吸收到電子質量項和電荷項之中,而成為有限的,從而可以與實驗結果相比較。理論計算的電子反常磁矩和
蘭姆移位與實驗值符合得極好。量子電動力學成為一門非常精確的理論。
在量子場論發展的早期,人們發現許多圈圖(即微擾展開的高階項)的計算結果含有發散(即無窮大)項。重正規化是解決這個困難的一個方案。一個理論如果只有有限種發散項,則可以在拉氏量中引進有限數目的項來抵消這些無窮大項,這種情形被稱為可重整。反之,如果理論中有無限種發散項,則稱為不可重整。
可重正規化曾被認為一個場論所必需滿足的自洽性要求。它在
量子電動力學和量子規範場論的發展過程中起過重要的作用。粒子物理的
標準模型也是可重整的。
現代場論的觀點認為所有理論都只是有效理論,它們都有它們的適用範圍。除了所謂的
終極理論,所有理論在原則上都是不可重整的。在這種觀點下,重正規化只是聯繫不同能標下理論的一種方法。
為了消除發散,把積分下限分別改為無窮小的
和
,這樣積分就變成了
如果能保證
那么就可以得到
求解
從另一種觀點看,可以在三維動量空間中表示狄拉克方程的解,其中與時間有關的項可以表示為:
其中n是微擾展開式的階次,由於散射矩陣表示的是始態(
) 和終態(
)之間的關係,兩態間的時間差是
,所以就會有:
這樣就說明了QED中的無窮大是始態和終態之間無窮大的時間差造成的,如果能計算微擾展開式的所有階次,那么無窮大和無窮大就會彼此相互抵消。例如函式
當x→∞時等式右邊的每一項(第一項1除外)都會趨向於無窮大,但所有項疊加的結果exp(-x^2)卻會趨向於零,這是因為無窮大與無窮大之間會彼此相互抵消。 微擾展開式的零階項中,時間項為exp(-ita); 一階項中,時間項為exp(-ita)-1; 二階項中,時間項為exp(-ita)-1-(-ita);顯然,從二階展開式開始,計算結果開始隨時間而發散,這也說明了為什麼無窮大不會出現在0階和1階展開式中,從二階展開式才開始出現無窮大。
發展過程
1965年,
朝永振一郎(Sin-Itiro Tomonaga)因在量子電動力學基礎理論研究方面的成就,與
施溫格(Julian Schwinger)、
費因曼(Richard Feynman)共同獲得
諾貝爾物理學獎。朝永振一郎最大的研究成果為
重整化理論與
中子研究、並且因為重整化理論而獲得諾貝爾物理學獎。
在70年代以前,人們知道的可以重正化的定域量子場論除量子電動力學外,還有贗標介子與核子相互作用理論,標量介子與核子相互作用理論,零自旋玻色子的電動力學,中性矢量玻色子(有時稱重光子)與守恆的媡/2自旋費密子流耦合的理論,無靜止質量的楊-密耳斯場(見規範場)的理論。但那時還不知道如何對有靜止質量的楊-密耳斯場理論以及帶電荷的規範場粒子的電磁相互作用理論進行重正化。
70年代初,G.
霍夫特(1971)、M.維爾特曼與霍夫特合作(1972)、B.W.李·J.津恩·朱斯坦(1972 Lee-Zinn-Justin)的一系列工作,說明了
楊·米爾斯場如果在
黑格斯機制下獲得靜止質量,則整個理論(理論中還可包括與黑格斯場耦合而獲得靜止質量的費密場)是可以重正化的。其中楊·米爾斯場還可以推廣到更一般的規範場。
由於這一發現,S.L.
格拉肖、S.
溫伯格和A.
薩拉姆在規範場理論前提下提出的電弱統一理論終於成為一個可以重正化的關於弱相互作用和電磁相互作用的統一理論。這個理論所預言的傳遞弱相互作用的粒子 W+、W-和Z0,都已於1983年被找到。
在這些成功的推動下,人們又認識到強相互作用可能也是一種由規範場傳遞的相互作用,因而提出了
量子色動力學(QCD)理論,這個理論在相當大的程度上與高能物理實驗結果相符,而且也是可以重正化的。這在強相互作用的研究中是一個創舉。
人們也嘗試著在量子規範理論的前提下把弱相互作用、電磁相互作用和強相互作用統一起來(見大統一理論),但其中還有不少問題有待澄清。
正規化
量子化的定域的引力理論的消除發散和重正化,是一個還沒有解決的問題。
實現重正化需進行正規化和剪除交纏無窮大。
正規化是用包含可調節參量的不發散積分取代發散積分,當可調節參量趨於某個極限時,這個不發散積分就還原為原來的發散積分。不發散積分又分為兩部分,當可調節參量趨於上述極限時,一部分仍保持不發散,另一部分趨於發散,從而把S 矩陣元中的發散部分和不發散部分分離開來。在正規化時要求;①選定一個以至一類確定的分離方式,把有限部分分離出來;②保持物理體系的對稱性;③原先不發散的積分在正規化後不改變。常用的正規化方法有:取質量M為可調節參量的費因曼法(1948);取若干個質量Mi為可調節參量的泡利-維拉斯法(1949);取空間、時間的維數n為可調節參量的維數正規化霍夫特-維爾特曼法(1972)。其中維數正規化法能滿足保持規範不變性的要求(有rs反常時除外),可稱為最佳方法。
舉例
只有正規化方法,而沒有合乎邏輯的處理交纏無窮大的方法,仍不能實現重正化。以量子電動力學為例,從費因曼圖可以看出,有些圖只有一個圈,如圖1。與圖對應的費因曼積分雖然都是發散的,但發散項的分離還比較簡單;雖然有些圖有共線的相鄰的圈,如圖2。與各個相鄰圈對應的費因曼積分都是發散的。這種圖形的發散稱為交纏發散或交纏無窮大。分離交纏無窮大的過程比較複雜,方法不止一種,層次分明、數學上較嚴格的方法是BPHZ法。其要點是首先對單圈子圖(費因曼圖中的一部分)的發散作減除,然後對雙圈子圖的發散作減除,依此遞推。這樣的減除等價於在拉格朗日量中依次引入能夠抵消一圈發散、雙圈發散、……、n 圈發散的各抵消項。
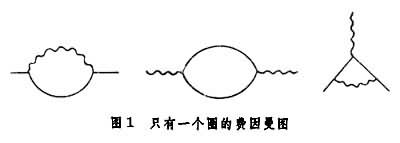 重正化1
重正化1量子規範理論(包括電弱統一理論、量子色動力學和大統一理論)的情況雖然比量子電動力學複雜,但它們的重正化問題都已解決。
在出現rs反常時,只要輕子的種類數和夸克的種類數相同,rs反常就自動相互抵消。
 重正化2
重正化2研究範圍
重正化是一個涉及面較廣的研究課題。粒子物理、統計物理等,都可遇到重正化問題。有一些很有意義的問題,如有束縛態時的重正化,彎曲時空量子場論的重正化等,都有待人們去深入探索。
現代的重正化理論並不只是被動地應付發散困難,它還能通過重正化群方法主動地給出物理上的新的預言。例如關於漸近自由預言。
重正化方法也有它的局限性,它不能解決微擾近似方法本身所固有的問題,如微擾級數收斂問題以及強耦合不能用微擾方法的問題等。
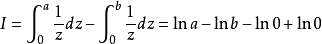


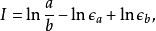

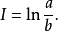
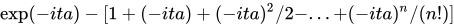
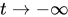

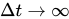


 重正化1
重正化1 重正化2
重正化2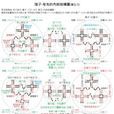
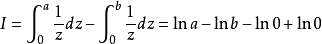


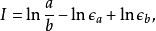

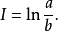
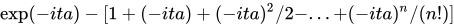
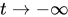

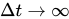


 重正化1
重正化1 重正化2
重正化2