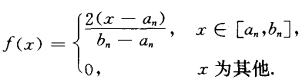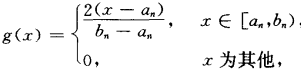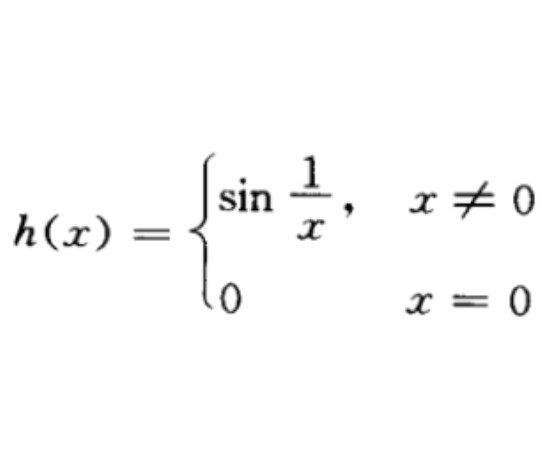基本介紹
定義 所謂函式f在[a,b]上具有介值性,是指任意x1,x2∈[a,b],y是介於f(x1)與f(x2)之間的任意一個數,則總有x3介於x1與x2之間,使y=f(x3).這時我們稱f在[a,b]上是Darboux函式,簡稱D函式,記為f∈D。
所謂函式f具有無窮介值性,記為f∈D*是指上述定義中,有無窮多個x3,介於x1與x2之間,使y=f(x3)。
所謂函式f具有c介值性,記為f∈D**是指上述定義中,有c個x3,介於x1與x2之間,使y=f(x3),其中c為連續統之勢。
因為連續函式具有介值性,故有關係
,具有c介值性必有無窮介值性更有介值性,因此
。
【例1】 連續函式有介值性,但有介值性函式未必連續。如函式
具有介值性,但在0點不連續,(o,1]中沒有無窮介值性,更無c介值性。
設P為[0,1]中Cantor集,{(an,bn)}為P的接鄰區間全體,f與g為:
達布連續函式的性質
1.由
介值定理,定義在區間上的連續函式必是達布連續的,但反之不一定成立。
例如,由f(x)=sin(1/x)(x≠0)與f(0)=0定義在[-1,1]上的函式f達布連續,但在x=0處不連續。
2.f:[a,b]→R達布連續的
充分必要條件是f把[a,b]的任何閉子區間映為區間或一個點。
3.達布連續函式的複合是達布連續的,因此,f(x)達布連續時,|f(x)|,f(x),cf(x) (c∈R),1/f(x) (f(x)≠0)也達布連續。
4.對於單調函式而言,達布連續與連續是等價的。
5.若f:R→R,且f在每個x∈R處的左、右極限存在,則f達布連續若且唯若f連續。
6.達布連續函式之和不一定達布連續。
7.達布連續函式列的一致極限不一定達布連續。
10.任何函式f∶R→R是兩個達布連續函式之差。
歷史上有些數學家曾以為介值性與連續性是等價的,
達布((J.-)G.Darboux)澄清了這兩個概念的差別。