連鎖推理(sorites)是複合三段論的省略形式之一,它在一個複合三段論中,只提出最後一個總的結論,而省略其他各三段論的結論,與複合三段論相應,它也有兩種形式。
基本介紹
- 中文名:連鎖推理
- 外文名:sorites
- 所屬學科:數學
- 所屬問題:形式邏輯
- 簡介:複合三段論的省略形式之一
- 兩種形式:前進連鎖推理,後退連鎖推理
基本介紹
前進連鎖推理
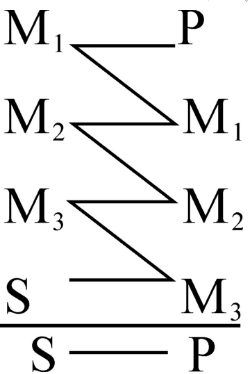 圖1
圖1後退連鎖推理
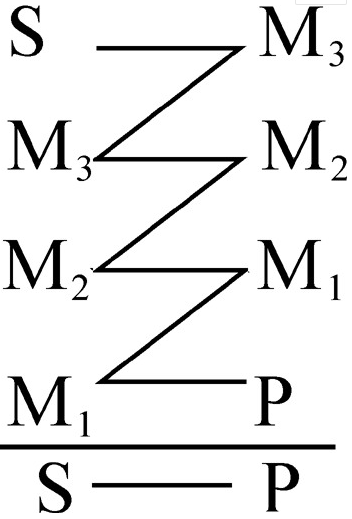 圖2
圖2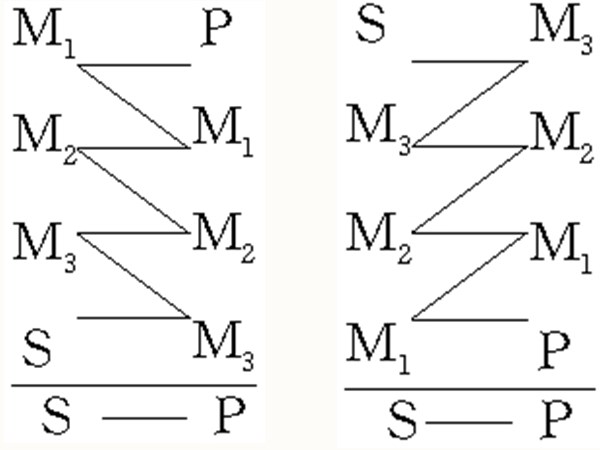
連鎖推理(sorites)是複合三段論的省略形式之一,它在一個複合三段論中,只提出最後一個總的結論,而省略其他各三段論的結論,與複合三段論相應,它也有兩種形式。
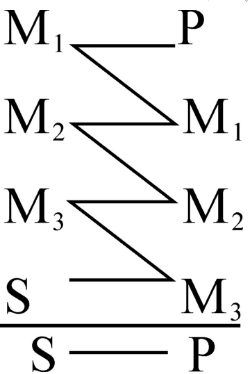 圖1
圖1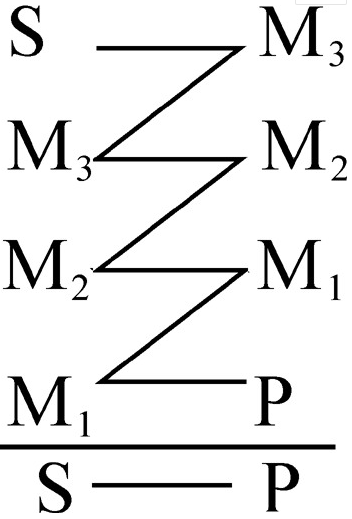 圖2
圖2連鎖推理(sorites)是複合三段論的省略形式之一,它在一個複合三段論中,只提出最後一個總的結論,而省略其他各三段論的結論,與複合三段論相應,它也有兩種形式。...
假言連鎖推理(hypothetical chain inference)亦稱連鎖式的假言推理、純假言推理,是一種複合推理,指由多個假言命題為前提,而推出一個假言命題結論的推理。假言連鎖推理...
連鎖三段論(sorites)是複合三段論的簡略形式。在連鎖三段論中,除留下最後得出的結論外,省去了複合三段論中作為中介的三段論結論。與複合三段論的兩種形式相對應,連鎖...
連鎖悖論(sorites paradox)是古希臘麥加拉學派歐布里德和阿萊克西努提出的一系列疑難中的一種。指一個微小量的連續相加或相減,最後達到一個不同質的事物。這是由...
推理是指個體在頭腦中根據已有的判斷,通過分析和綜合引出新判斷的過程。...... 選言和複合推理的正確率達到62.5%,連鎖推理的正確率為48%,高一學生(約16歲)的推理...
《向福爾摩斯學習推理能力》精選了150箇中外經典探案故事,這些故事驚險曲折、扣人心弦,融知識性、趣味性於一體。書中首先對故事按照常識推理、科學推理、細節推理、...
《邏輯推理集錦》...... 將若干個相關的假言推理連線起來,使前一個假言推理的結論成為後一個假言推理的前提,就就可形成一個純假言連鎖推理。...
《FBI推理術:美國聯邦警察破案精華,幫你提高邏輯推理能力》是由中國法制出版社於2013-02-01出版的圖書,本書作者是崔明磊。...
假言連鎖推理法(hypothetical chain inference)亦稱連鎖式的假言推理、純假言推理,是一種複合推理,指由多個假言命題為前提,而推出一個假言命題結論的推理。假言連鎖...
典型的連鎖推理形式如亞里士多德式:所有A是B,所有B是C,所有C是D,所以,所有A是D;哥克蘭尼式:所有C是D,所有B是C,所有A是B,所以,所有A是D。關於連鎖推理更為...
1.6.1 什麼是二難推理1.6.2 難推理的形式1.6.3 Z.難推理的套用1.7 其他複合命題推理1.7.1 假言聯言推理1.7.2 假言連鎖推理...
第六節 多重複合命題推理訓練一、反三段論/156二、假言連鎖推理/162三、假言選言推理(二難推理)/170第七節 模態命題及推理訓練一、根據模態邏輯方陣進行的模態...
