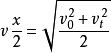定義
加速度 (acceleration) 表征單位時間內速度改變程度的矢量。一般情況下,加速度是個瞬時概念,它的常用單位是米/秒2、m/s2等。
在最簡單的勻加速直線運動中,加速度的大小等於單位時間內速度的增量。若動點的速度v1經t秒後變成v2,則其加速度可表示為:
動點Q做一般空間運動時,速度矢量的變化和所經時間△t的比,稱為△t時間內的平均加速度(圖1),記為a平:
當時間間隔△t趨於零時,平均加速度的極限稱為瞬時加速度(圖1),簡稱加速度,記為a:
因而加速度的嚴格定義為:加速度矢量等於速度矢量對時向的導數,其方向沿著速端圖的切線方向並指向軌跡的凹側。關於加速度產生的原因,可參見牛頓運動定律。
單位
m/s2 或m·s-2(米每二次方秒)
加速度是矢量,既有大小又有方向。(方向由+、-號代表)
加速度的大小等於單位時間內速度的改變數;加速度的方向與速度變化量ΔV方向始終相同。特別,在直線運動中,如果加速度的方向與速度相同,速度增加;加速度的方向與速度相反,速度減小。
加速度等於對速度時間的一階導數,等於位移對時間的二階導數
物理意義
表示質點速度變化的快慢的物理量。
舉例:假如兩輛汽車開始靜止,均勻地加速後,達到10m/s的速度,A車花了10s,而B車只用了5s。它們的速度都從0變為10m/s,速度改變了10m/s。所以它們的速度變化量是一樣的。但是很明顯,B車變化得更快一些。我們用加速度來描述這個現象:B車的加速度(
a=Δv/Δt,其中的Δv是速度變化量)>A車的加速度。
 加速度計構造的類型
加速度計構造的類型顯然,當速度變化量一樣的時候,花時間較少的B車,加速度更大。也就是說B車的啟動性能相對A車好一些。因此,加速度是表示物體速度變化快慢的物理量。
注意
1.當物體的加速度保持大小不變時,物體就做勻變速運動。如自由落體運動、平拋運動等。
當物體的加速度方向與大小在同一直線上時,物體就做勻變速直線運動。如豎直上拋運動。
2.加速度可由速度的變化和時間來計算,但決定加速度的因素是物體所受合力F和物體的質量M。
3.加速度與速度無必然聯繫,加速度很大時,速度可以很小;速度很大時,加速度也可以很小。例如:炮彈在發射的瞬間,速度為0,加速度非常大;以高速直線勻速行駛的賽車,速度很大,但是由於是勻速行駛,速度的變化量是零,因此它的加速度為零。
4.加速度為零時,物體靜止或做勻速直線運動(相對於同一參考系)。任何複雜的運動都可以看作是無數的勻速直線運動和勻加速運動的合成。
5.加速度因參考系(參照物)選取的不同而不同,一般取地面為參考系。
6.當運動物體的速度方向與加速度(或合外力)方向之間的夾角小於90°時,速率將增大,速度的方向將改變;
當運動物體的速度方向與加速度(或合外力)方向之間的夾角大於90°而小於或等於180°時,速率將減小,方向將改變;
當運動物體的速度和方向與加速度(或合外力)方向之間的夾角等於90°時,速率將不變,方向改變。
7.力是物體產生加速度的原因,物體受到外力的作用就產生加速度,或者說力是物體速度變化的原因。說明當物體做
加速運動(如自由落體運動)時,加速度為正值;當物體做減速運動(如豎直上拋運動)時,加速度為負值。
8.加速度的大小比較只比較其絕對值。物體加速度的大小跟
作用力成正比,跟
物體的質量成反比,加速度的方向跟作用力的方向相同,負號僅表示方向,不表示大小。
向心加速度
向心加速度(勻速圓周運動中的加速度)的計算公式:
 科里奧利加速度
科里奧利加速度 a=rω2=v2/r
說明:a就是向心加速度,推導過程並不簡單,但可以說仍在高
中生理解範圍內,這裡略去了。r是
圓周運動的半徑,v是速度(特指
線速度)。ω(就是歐姆的小寫)是
角速度。
這裡有:v=ωr.
1.
勻速圓周運動並不是真正的
勻速運動,因為它的速度方向在不斷的變化,所以說勻速圓周運動只是勻
速率運動的一種。至於說為什麼叫他勻速圓周運動呢?可能是大家說慣了不願意換了吧。
2.勻速圓周運動的向心加速度總是指向圓心,即不改變速度的大小只是不斷地改變著速度的方向。
3. 勻速圓周運動也不是勻變速運動,向心加速度的方向也在不斷改變,但永遠指向圓心且大小不變。
重力加速度
重力加速度g的方向總是豎直向下的。在同一地區的同一高度,任何物體的重力加速度都是相同的。重力加速度的數值隨
海拔高度增大而減小。當物體距地面高度遠遠小於
地球半徑時,g變化不大。而離地面高度較大時,重力加速度g數值顯著減小,此時不能認為g為常數
距離地面同一高度的重力加速度,也會隨著緯度的升高而變大。由於重力是
萬有引力的一個
分力,萬有引力的另一個分力提供了物體繞地軸作圓周運動所需要的
向心力。物體所處的地理位置緯度越高,
圓周運動軌道
半徑越小,需要的向心力也越小,重力將隨之增大,重力加速度也變大。地球南北兩極處的圓周運動軌道半徑為0,需要的向心力也為0,重力等於萬有引力,此時的重力加速度也達到最大。
由於g隨緯度變化不大,因此國際上將在緯度45°的海平面精確測得物體的重力加速度g=9.80665m/s2;作為重力加速度的標準值。在解決地球表面附近的問題中,通常將g作為常數,在一般計算中可以取g=9.80m/s2。理論分析及精確實驗都表明,隨緯度增大,重力加速度g的數值逐漸增大。如:
赤道g=9.780m/s2
廣州g=9.788m/s2
武漢g=9.794m/s2
上海g=9.794m/s2
東京g=9.798m/s2
北京g=9.801m/s2
紐約g=9.803m/s2
莫斯科g=9.816m/s2
北極g=9.832m/s2
註:月球表面的重力加速度約為1.62 m/s2,約為地球表面重力加速度的六分之一。
勻加速直線運動公式
1.勻加速直線運動的位移公式:
2.勻加速直線運動的速度公式:
3.勻加速直線運動的平均速度(也是中間時刻的瞬時速度):
4.勻加速度直線運動的幾個重要推論:
(以
初速度方向為正方向,勻加速直線運動,a取正值; 勻減速直線運動,a取負值。)
(2) 時間中點的瞬時速度等於平均速度:
(3) AB段位移中點的即時速度:
(4) 初速為零的勻加速直線運動,在前1s ,前2s,前3s……前ns內的位移之比為1^2:2^2:3^2……:n^2;
(5) 在第1s 內,第 2s內,第3s內……第ns內的位移之比為1:3:5……:(2n-1);
(6)在前1米內,前2米內,前3米內……前n米內的時間之比為1:2^(1/2):3^(1/2):……:n^(1/2)
(7) 初速無論是否為零,勻變速直線運動的質點,在連續相鄰的相等的時間間隔內的位移之差相等,為一常數:△x= aT2(a一勻變速直線運動的加速度 T一每個時間間隔的時間)。
(8)
豎直上拋運動: 上升過程是勻減速直線運動,下落過程是勻加速直線運動。全過程是初速度為VO,加速度為g的勻減速直線運動。
速度與加速度
物體運動時,如果加速度不為零,則處於變速狀態。若加速度大於零,則為加速(即加速度和速度方向相同);若加速度小於零,則為減速(即速度和加速度方向相反)。(提示:物理中的符號不同於數學中的符號,在數學中+、-號只代表是的標量,在物理中+、-號部分代表方向)
曲線加速運動
在加速度保持不變的時候,物體也有可能做
曲線運動。比如,當你把一個物體沿水平方向用力拋出時,你會發現,這個物體離開桌面以後,在空中划過一條曲線,落在了地上。
物體在出手以後,受到的只有
豎直向下的重力,因此加速度的方向和大小都不改變。但是物體由於
慣性還在水平方向上以出手速度運動。這時,物體的速度方向與加速度方向就不在同一直線上了。物體就會往力的方向偏轉,划過一條往地面方向偏轉的曲線。
但是這個時候,由於重力大小不變,因此加速度大小也不變。物體仍然做的是
勻加速運動,但不過是勻加速
曲線運動。
量綱
加速度可以有不同的單位,但其量綱是唯一的,即:L*T^(-2) 加速度也就是速度變化率



 加速度計構造的類型
加速度計構造的類型 科里奧利加速度
科里奧利加速度







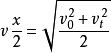




 加速度計構造的類型
加速度計構造的類型 科里奧利加速度
科里奧利加速度