輾轉相除

輾轉相除，又名歐幾里德算法（Euclidean algorithm），乃求兩個正整數之最大公約數的算法。它是已知最古老的算法, 其可追溯至公元前300年。

基本介紹

• 中文名：輾轉相除
• 外文名：Euclidean algorithm
• 又名：歐幾里德算法
• 簡介：求兩個正整數之最大公約數的算法

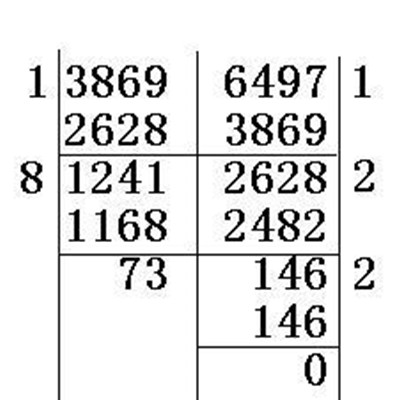
簡介

它是已知最古老的算法, 其可追溯至公元前300年。它首次出現於歐幾里德的《幾何原本》（第VII卷，命題i和ii）中，而在中國則可以追溯至東漢出現的《九章算術》。它並不需要把二數作質因子分解。

算法內容

輾轉相除法是利用以下性質來確定兩個正整數 a 和 b 的最大公約數的：

1. 若 r 是 a ÷ b 的餘數, 則

gcd(a,b) = gcd(b,r)

2. a 和其倍數之最大公約數為 a。

另一種寫法是：

1. a ÷ b，令r為所得餘數（0≤r<b）

若 r = 0，算法結束；b 即為答案。

2. 互換：置 a←b，b←r，並返回第一步。

算法證明

證明：

已知m=qn+p，即m整除n的商為q，餘數為p（其中,m≥n,n>p）。

注意：使用(m,n)表示m和n的最大公約數；(n,p)表示n和p的最大公約數.用m|n表示m為n的因數。

對於任意的m和n的公因數r，都有r|m和r|n。根據等式m=qn+p，可知r|p（因為等式可寫成ra=rbn+p），則r為n和p的公因數。

因此，所有m和n的公因數，都是n與p的公因數。

同理可得，所有n與p的公因數，都是m與n的公因數。

因此，（m，n）=（n，p），即m與n的最大公因數為n與m整除n後的餘數q的最大公因數。

則對於任意兩個整數a，b（其中a>=b），其最大公因數為a整除b後的餘數與b的最大公因數。

得證。

代碼

計算機代碼如下：

其中“a mod b”是指取 a ÷ b 的餘數

function gcd(a, b) {if a mod b<>0return gcd(b, a mod b);elsereturn b;}//或純使用循環:function gcd(a, b) {define r as integer;while b ≠ 0 {r := a mod b;a := b;b := r;}return a;}

。

例如，123456 和 7890 的最大公因子是 6, 這可由下列步驟看出：

a b a mod b

123456 7890 5106

7890 5106 2784

5106 2784 2322

2784 2322 462

2322 462 12

462 12 6

12 6 0

只要可計算餘數都可用輾轉相除法來求最大公約數。這包括多項式、復整數及所有歐幾里德定義域（Euclidean domain）。

C程式：

int m,n;scanf("%d%d",&m,&n);int a = m,b = n;//8 12//8 % 12  8//12 % 8  4//8 % 4   0//12 8//12 % 8  4//8 % 4   0while (m % n != 0) {int temp = m % n;m = n;n = temp;}printf("%d %d\n",n,a * b / n);

輾轉相除法的運算速度為 O(n²)，其中 n 為輸入數值的位數。