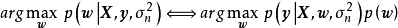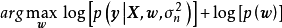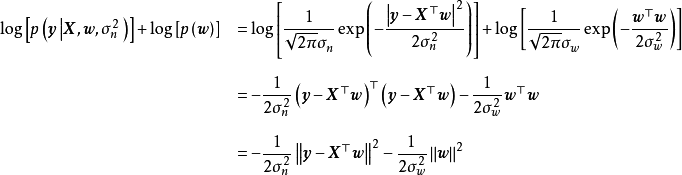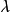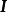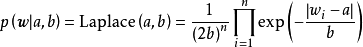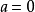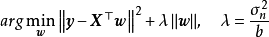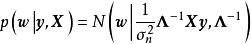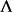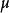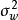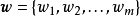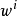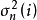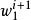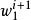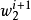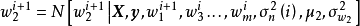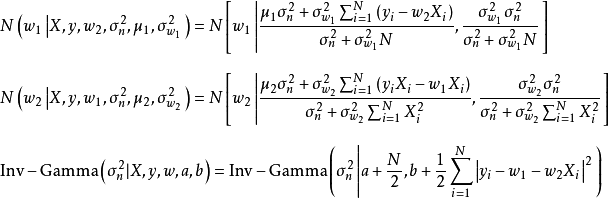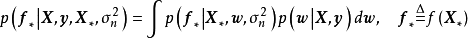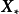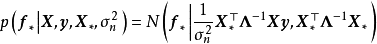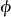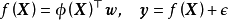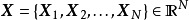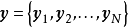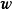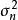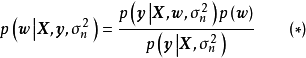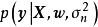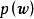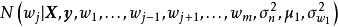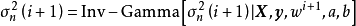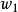5. 重複1-4至疊代完成/分布收斂
import numpy as npimport matplotlib.pyplot as plt# 構建測試數據## 自變數:[0,5]區間均勻分布x = np.random.uniform(low=0, high=5, size=5)## 因變數:y=2x-1+eps, eps=norm(0, 0.5)y = np.random.normal(2*x-1, 0.5)def calculate_csd(x, y, w1, w2, s, N, hyper_param): ''' 條件採樣分布函式: (w1, w2, s) x , y: 輸入數據 w1, w2: 線性回歸模型的截距和斜率 s: 殘差方差 N: 樣本量 ''' # 超參數 mu1, s1 = hyper_param["mu1"], hyper_param['s1'] mu2, s2 = hyper_param["mu2"], hyper_param['s2'] a, b, = hyper_param["a"], hyper_param["b"] # 計算方差 var1 = (s1*s)/(s+s1*N) var2 = (s*s2)/(s+s2*np.sum(x*x)) # 計算均值 mean1 = (s*mu1+s1*np.sum(y-w2*x))/(s+s1*N) mean2 = (s*mu2+s2*np.sum((y-w1)*x))/(s+s2*np.sum(x*x)) # 計算(a, b) eps = y-w1-w2*x a = a+N/2; b = b+np.sum(eps*eps)/2 # 使用numpy.random採樣(inv-gamma=1/gamma) # 注意numpy.random中normal和gamma的定義方式: ## np.random.normal(mean, std) ## inv-Gamma = 1/np.random.gamma(a, scale), scale=1/b return np.random.normal(mean1, np.sqrt(var1)), \ np.random.normal(mean2, np.sqrt(var2)), \ 1/np.random.gamma(a, 1/b)def Gibbs_sampling(x, y, iters, init, hyper_param): ''' 吉布斯採樣算法主程式 iter: 疊代次數 init: 初始值 hyper_param: 超參數 ''' N = len(y) # 樣本量 # 採樣初始值 w1, w2, s = init["w1"], init["w2"], init["s"] # 使用數組記錄疊代值 history = np.zeros([iters, 3])*np.nan # for循環疊代 for i in range(iters): w1, w2, s = calculate_csd(x, y, w1, w2, s, N, hyper_param) history[i, :] = np.array([w1, w2, s]) return history# 開始採樣iters = 10000 # MCMC疊代1e4次init = {'w1': 0, 'w2': 0, 's': 0}hyper_param = {'mu1': 0, 's1': 1, 'mu2': 0, 's2': 1, 'a': 2, 'b': 1}history = Gibbs_sampling(x, y, iters, init, hyper_param)burnt = history[500:] # 截取收斂後的馬爾可夫鏈ax1 = plt.subplot(2, 1, 1); ax2 = plt.subplot(2, 1, 2)ax1.hist(burnt[:, 0], bins=100)ax1.text(2, 0.025*iters, '$\mathrm{N(w_1|\mu,s)}$', fontsize=14)ax2.hist(burnt[:, 1], bins=100)ax2.text(.5, 0.025*iters, '$\mathrm{N(w_2|\mu,s)}$', fontsize=14)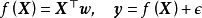



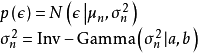


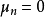
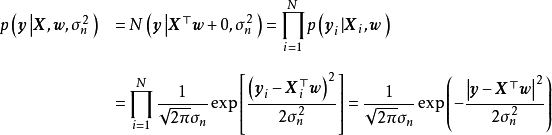
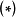
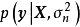

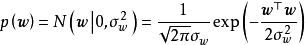
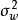
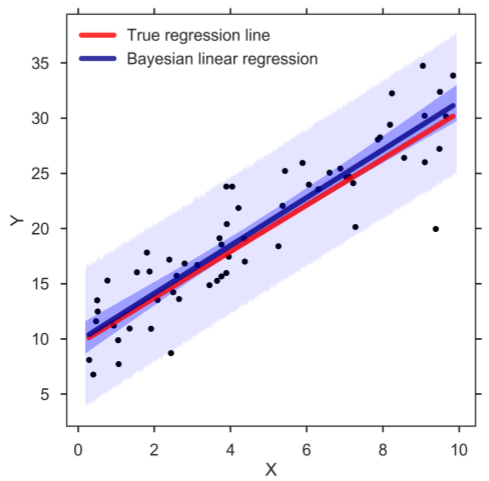
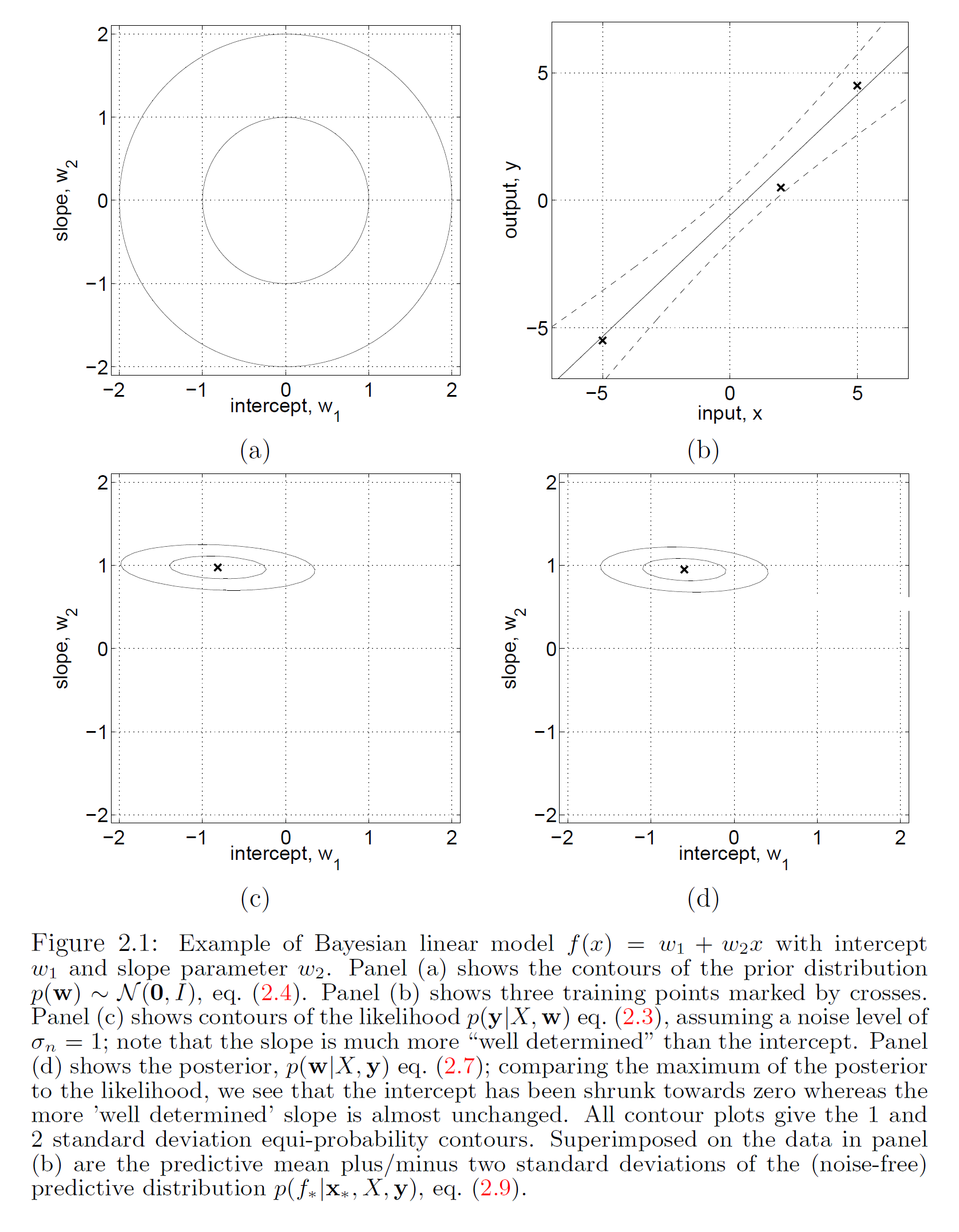 一維貝葉斯線性回歸:(a,c,d)先驗、似然和後驗,(b)回歸結果
一維貝葉斯線性回歸:(a,c,d)先驗、似然和後驗,(b)回歸結果