基本介紹
- 中文名:隨機效應模型
- 外文名: random effects models
- 簡稱:REM
- 學科:數學
- 釋義:固定效應的回歸係數看作隨機變數
- 相關概念:固定效應模型、混合效應模型
簡介
隨機效應模型的用途
與固定效應模型(FEM)的比較
從定義的角度
基於統計學角度

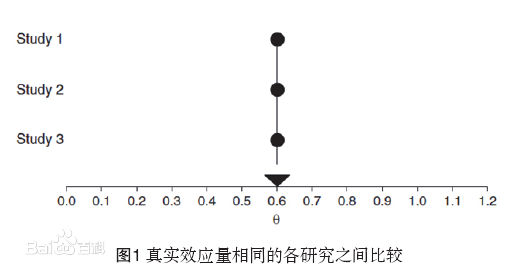 圖1
圖1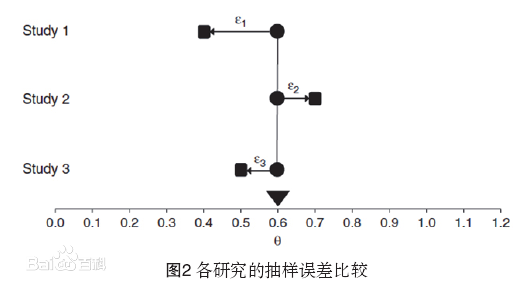 圖2
圖2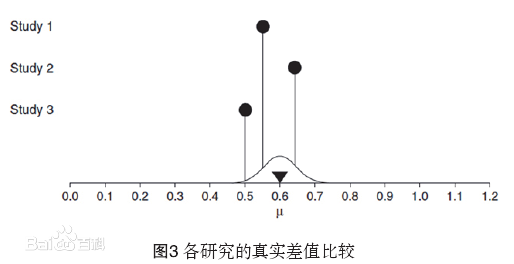 圖3
圖3 圖4
圖4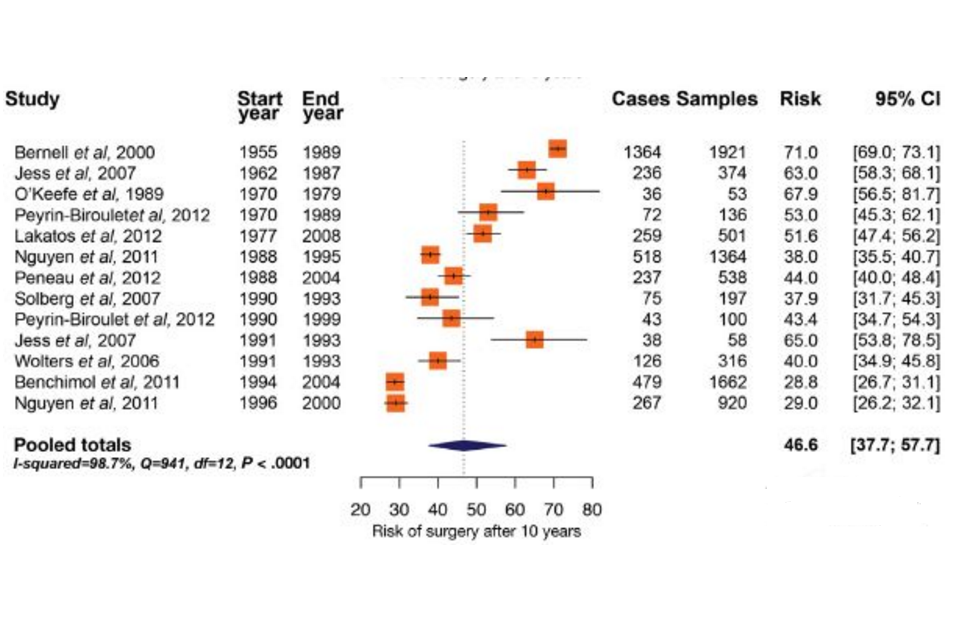

 圖1
圖1 圖2
圖2 圖3
圖3 圖4
圖4隨機效應模型(random effects models),簡稱REM,是經典的線性模型的一種推廣,就是把原來(固定效應模型)的回歸係數看作是隨機變數,一般都是假設是來自常態分配。如果...
固定效應模型(fixed effects model),即固定效應回歸模型,簡稱FEM,是一種面板數據分析方法。它是指實驗結果只想比較每一自變項之特定類目或類別間的差異及其與其他...
隨機效應:就是我們的樣本從一個很大的母體抽取,所以大家的期望(均值)相同;如果我們的樣本幾乎是全部母體了,我們就不能說個體的差異是隨機的,所以固定效應比較好;...
混合線性模型(mixed linear model)是一種方差分量模型。在方差分量模型中,把既含有固定效應,又含有隨機效應的模型,稱為混合線性模型。...
隨機分量模型亦稱隨機方差分量模型、隨機因子方差分析模型、方差分析模型Ⅱ,是主效應或互動效應都是隨機變數的方差分析模型,描繪各因子水平都是隨機選取的方差分析模型...
混合模型(hybrid model)是幾種不同模型組合而成的一種模型。它允許一個項目能沿著最有效的路徑發展。也可定義為由固定效應和隨機效應(隨機誤差除外)兩部分組成的...
《固定效應回歸模型》是2012年格致出版社出版的圖書,作者是保爾·D.埃里森。...... 此外,“固定效應模型”這一概念還經常與“隨機效應模型”形成對照,作者在《固定...
系統分量模型即固定效應模型,亦稱系統方差分量模型、方差分析模型I。“隨機效應模型”的對稱。主效應和互動效應都是常數的方差分析模型,描繪因子水平可以完全控制的析...
本書分別就面板數據的靜態模型,動態模型、單位根和協整分析,受限因變數、變係數模型和隨機前沿模型等六大領域進行了全面探討,側重介紹靜態模型、動態模型、單位根和...
《混合效應模型在林業建模中的套用》是關於線性和非線性混合效應模型理論、方法及其在林業建模上套用的專著。內容主要介紹單水平和多水平統計模型。將單水平混合效應...
亦稱隨機方差分量模型、隨機因子方差分析模型、方差分析模型II。主效應或互動效應部是隨機變數的方差分析模型,描繪各因子水平都是隨機選取的方差分析模型。對於隨仉效應...
根據統計假設的不同可將Meta 分析方法分為兩類:固定效應模型和隨機效應模型,前者假設所有研究享有共同的真實效應大小,後者假設所有研究的真實效應大小不同,具體體現在...
在異質性較大時,隨機效應模型主要是校正合併效應值的算法,使得結果更加接近無偏估計,即結果更為準確,但其得出的結論偏向於保守,置信區間較大,更難以發現差異,如果...
+因素n主效應+因素互動效應1+因素互動效應2+…+因素互動效應m+隨機誤差。所以多因素方差分析往往選用一般化線性模型(General Iinear Model)進行參數估計 [1] 。...
