基本簡介
假設我們進行一系列的實驗,這些實驗之間是與統計無關的,而且每個實驗僅有兩種可能的結果,設所有這些實驗取得兩個中的任一結果的機率都是一樣的。例如,當投擲一個硬幣時,那么可能的結果就是頭像朝上和頭像朝下。在理想的情況下,如果這些實驗滿足所說的條件,我們就稱它為“貝努利實驗”。這種實驗包含幾次獨立試驗,且每次試驗中只有兩種可能結果:成功或失敗;又被稱為二次實驗。
重複進行n次獨立的貝努利試驗,這裡“重複”的意思是指各次試驗的條件是相同的,它意味著各次試驗中事件發生的機率保持不變,“獨立”的意思是指是指各次試驗的結果是相互獨立的,這種試驗所對應的數學模型成為貝努利概型。有時為了突出實驗次數n,也稱為n重貝努利試驗。
目標
討論貝努力試驗最終的目的乃建立一模型,據此模型可求得當我們重複進行此種試驗時,兩種結果之一(成功或失敗)可能出現的次數。
當某種試驗連續且重複進行時,每一次重複的實驗稱為一個試驗。此外,一個試驗可能出現兩個結果,分別稱為成功(S)與失敗(F)。再次特彆強調的是,此種試驗下只有兩種可能結果,但並非取其成功或失敗的字面上的意義。習慣上,將某研究中我們所關心的事件標記為成功(即使是一個悲慘的事件),例如,研究失業率的問題中,我們往往將失業的事件視為兩種結果之一的“成功”事件。
貝努利模型
我們做n次實驗。每次實驗能以機率p出現事件A或者以機率q=1-p出現與A對立的事件
,且這n次實驗的秸果是相互獨立的。我們指定數1代表事件A出現,數0代表事件
出現。在n次實驗中,事件4可能出現0,1,2,…,n次。以X=k表示在n次實驗中事件A恰好出現k次的事件,因此隨機變數X能取值k=0,1,2,…,n。
這個隨機數的機率函式可以表示如下:
定理
說明
如果我們把貝努利試驗中某種結果稱為成功或是失敗的,而且只是關心n次貝努利試驗中總的成果次數,而不關心它出現的次序,那么在n次貝努利試驗中,k次成功可以有
種方式分布。
如果每次成功的機率是p,那么失敗的機率是q=1-p,出現k次成功的每一種方式的機率是
,而表示這種成功的分布函式稱為“二項式分布函式”。
注意
各個實驗是獨立的,說明某一次試驗中成功的幾率,並不受其它試驗所獲得訊息的影響;
每一次試驗只可能出現兩個結果,分別稱為成功(S)與失敗(F)
定理
n次貝努利試驗中,每次成功的機率為p,失敗的機率為q=1-p,k次成功和n-k次失敗(0≤k≤n)的機率為:
證明
假設進行n次貝努利試驗時,用n元組(a1,a2,a3,…an)表示結果,其中ai=S表示成功,ai=F表示失敗,i=1,2,3,4,5,…,n。
由於n次試驗是獨立的,是由k次成功和n-k次失敗組成的,所以每個n次實驗結果的機率為
,而由S和F構成的包含k個S和n-k個F的n元組有個,所以k次成功和n-k次失敗(0≤k≤n)的機率為:
我們可以把成功機率為p,失敗機率為q=1-p的n次獨立的伯努利實驗中有k次成功和n-k次失敗的機率記為
,且有
。
套用
一個工廠希望生產的產品中次品只有10%,採用的質量控制方法是由在40個產品的一次採樣中計算次品的數目組成,經過400採樣後,所得結果如下:
 採樣結果
採樣結果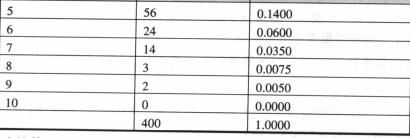 採樣結果
採樣結果“成功”應該算是找到一個次品,這裡我們計算每40個試驗中成功的次數,因為“成功”的機率為p=0.1,雖然我們不能期望每次都正好有10%的次品,但是,這個分布符合二項式分布:
雖然400是一個比較少的採樣數,但是實驗證明理論和實際符合得相當好,下表所示是實際的數據,和理論的數據相符合。
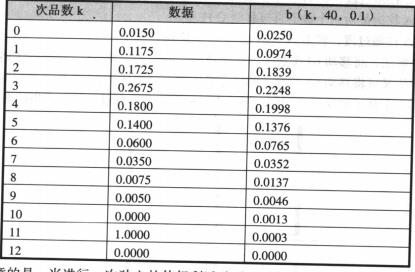 實際的數據和理論的符合情況
實際的數據和理論的符合情況



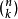


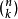




 採樣結果
採樣結果 採樣結果
採樣結果
 實際的數據和理論的符合情況
實際的數據和理論的符合情況