基本介紹
- 中文名:豪斯多夫測度
- 外文名:Hausdorff measure
- 所屬學科:數學
- 所屬問題:測度論(幾何測度論)
- 提出者:豪斯多夫
基本介紹
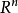
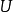
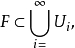
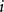
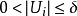

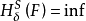
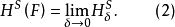

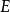
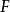
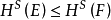
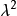
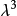
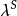
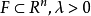
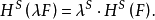
其他介紹
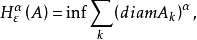
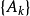
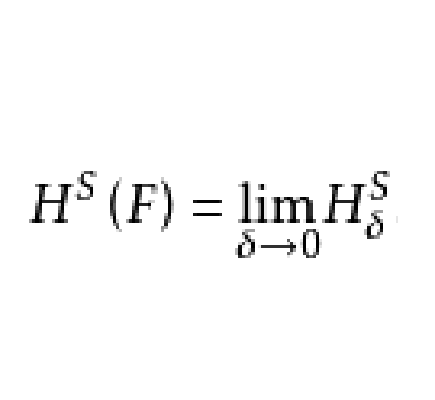
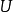
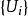
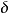

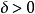
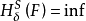
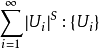
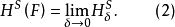
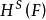

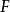
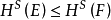
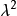
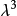
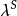
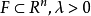
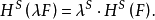
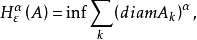
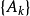
豪斯多夫測度(Hausdorff measure)是由豪斯多夫(F.Hausdorff)提出和命名的一種測度。為了定量地描述非整數維,豪斯多夫於1919年從測量的角度引進了豪斯多夫測度。該測度...
不能把豪斯多夫測度與豪斯多夫維數的概念混淆。可以證明,在無窮維空間不存在勒貝格測度的類似物。參考資料 1. [2]第二章 勒貝格測度_百度文庫 https://wenku....
豪斯多夫維又稱作豪斯多夫-貝塞科維奇維(Hausdorff-Becikovich Dimesion),它是由數學家豪斯多夫於1918年引入的。通過豪斯多夫維可以給一個任意複雜的點集合比如分形(...
拉東測度是一種正則測度。設B(Ω)是豪斯多夫空間Ω上的波萊爾集類,F是Ω上的σ代數且F⊃B(Ω),μ是F上的正則測度,C0(Ω)是Ω上有緊支集的實值連續函式...
豪斯多夫維數是分形幾何中最重要的一種維數。康托爾集的豪斯多夫維數為=log2/log3,其 s 維豪斯多夫測度為1。...
豪斯多夫,F.德國數學家。1868年11月8日生於布列斯勞(今波蘭弗拉茨瓦夫),1942年1月26日卒于波恩。幼時隨父母遷往萊比錫。1891年在萊比錫大學取得博士學位。1896年...
等人的研究則將單葉函式的邊界性質同像域邊界子集的豪斯多夫測度聯繫起來。 [1] 參考資料 1. 《數學辭海》總編輯委員會.《數學辭海》第3卷:東南大學出版社,...
5.4.1 豪斯多夫測度和豪斯多夫維數5.4.2 維數的幾種計算方法5.4.3 海面回波的分維數參考文獻第6章 粗糙面與目標的複合電磁散射6.1 矩量法在粗糙面與目標複合...
貝西科維奇研究擻谷(Kakeya)問題、殆周期函式、豪斯多夫測度、幾何測度論、表面面積、實分析和複變函數等,在殆周期函式等方面有重要貢獻.1919 年左右,他給出了...
2.1 豪斯多夫測度2.2 豪斯多夫維數2.3 豪斯多夫維數的計算——簡單的例子*2.4 豪斯多夫維數的等價定義*2.5 維數的精細定義2.6 註記和參考文獻...
