正則波萊爾測度

正則波萊爾測度(regular Borel measure)是正則的波萊爾測度。設Ω是豪斯多夫空間。如果μ是B(Ω)上的波萊爾測度且是正則的，則稱μ是B(Ω)上的正則波萊爾測度。

基本介紹

• 中文名：正則波萊爾測度
• 外文名：regular Borel measure
• 領域：數學
• 學科：測度論
• 性質：正則的波萊爾測度
• 空間：豪斯多夫空間

概念

正則波萊爾測度(regular Borel measure)是正則的波萊爾測度。設Ω是豪斯多夫空間。如果μ是B(Ω)上的波萊爾測度且是正則的，則稱μ是B(Ω)上的正則波萊爾測度。R上的勒貝格測度限制在波萊爾集類上是正則波萊爾測度。

測度

數學上，測度（Measure）是一個函式，它對一個給定集合的某些子集指定一個數，這個數可以比作大小、體積、機率等等。傳統的積分是在區間上進行的，後來人們希望把積分推廣到任意的集合上，就發展出測度的概念，它在數學分析和機率論有重要的地位。

測度論是實分析的一個分支，研究對象有σ代數、測度、可測函式和積分，其重要性在機率論和統計學中都有所體現。

定義1：構造一個集函式，它能賦予實數集簇М中的每一個集合E一個非負擴充實數mE。我們將此集函式稱為E的測度。

定義2：設Γ是集合X上一σ代數，ρ ：Γ →R∪{ +∽ }是一集合函式，且ρ滿足：

（1）（非負性）對任意的A∈Γ，有ρ(A)≧0;

（2）（規範性）ρ(Φ) = 0；

（3）（完全可加性） 對任意的一列兩兩不交集合A1，A2，……，An，……有：

則稱ρ是定義在X上的一個測度，Γ中的集合是可測集，不在Γ中的集合是不可測集。特別的，若ρ(X) = 1 ，則稱ρ為機率測度。

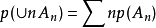
正則測度

正則測度是一種比較規則的測度。設Ω是豪斯多夫空間，B(Ω)是Ω上的波萊爾集類，F為Ω上包含B(Ω)的σ代數，μ是F上的測度。如果對每個A∈F，有：

則稱μ為外正則的;如果對每個開集G，有：

則稱μ為內正則的；既外正則又內正則的測度稱為正則測度。

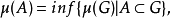
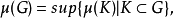
豪斯多夫空間

在拓撲學和相關的數學分支中，豪斯多夫空間、分離空間或T2 空間是其中的點都“由鄰域分離”的拓撲空間。在眾多可施加在拓撲空間上的分離公理中，“豪斯多夫條件”是最常使用和討論的。它蘊涵了序列、網和濾子的極限的唯一性。豪斯多夫得名於拓撲學的創立者之一費利克斯·豪斯多夫。豪斯多夫最初的拓撲空間定義把豪斯多夫條件包括為公理。

假設X是拓撲空間。設x和y是X中的點。如果存在 x 的鄰域 U 和 y 的鄰域 V 使得U和V是不相交的 (U ∩ V = ∅)，我們稱x和y可以“由鄰域分離”。X 是豪斯多夫空間如果任何兩個X 的獨特的點可以由鄰域分離。這時的豪斯多夫空間也叫做T2空間和分離空間的原因。

X 是預正則空間，如果任何兩個拓撲可區分的點可以由鄰域分離。預正則空間也叫做R1 空間。

在這些條件之間的聯繫如下。拓撲空間是豪斯多夫空間，若且唯若它是預正則空間和柯爾莫果洛夫空間的二者(就是說獨特的點是拓撲可區分的)。拓撲空間是預正則空間，若且唯若它的柯爾莫果洛夫商空間是豪斯多夫空間。

對於拓撲空間 X，以下論述等價：

X 是豪斯多夫空間。

是積空間的閉集。

X 中極限是唯一的(就是序列、網和濾子收斂於最多一個點)。

所有包含在 X 中的單元素集合都等於包含它的所有閉鄰域的交集。

對角的 Δ = {(x,x) | x ∈ X} 作為乘積空間 X × X 的子集是閉集。