自旋網路

量子力學中，自旋網路是一種圖表，用以表示粒子與量子場之間的的相互作用與狀態。以數學的出發點來看，這些圖案是一種簡明方法，可代表多線性函式以及矩陣群眾多表示之間的關聯函式。此圖案記號往往能簡化計算，以其能代表複雜的函式。自旋網路的發明一般是歸因於羅傑·彭羅斯於1971年的貢獻，[1]然而在此之前已有類似的圖樣方法。

基本介紹

• 中文名：自旋網路
• 外文名：Spin network
• 領域：量子力學

簡介

量子力學中，自旋網路是一種圖表，用以表示粒子與量子場之間的的相互作用與狀態。以數學的出發點來看，這些圖案是一種簡明方法，可代表多線性函式以及矩陣群眾多表示之間的關聯函式。此圖案記號往往能簡化計算，以其能代表複雜的函式。自旋網路的發明一般是歸因於羅傑·彭羅斯於1971年的貢獻，然而在此之前已有類似的圖樣方法。

透過卡洛·羅威利,李·斯莫林、霍爾黑·普林,羅多佛·甘比尼等多位研究者的努力，自旋網路被用於量子引力理論。自旋網路亦可被用在數學中局域規範轉換不變性的連通空間，用以建構特定的泛函。

彭羅斯原始定義

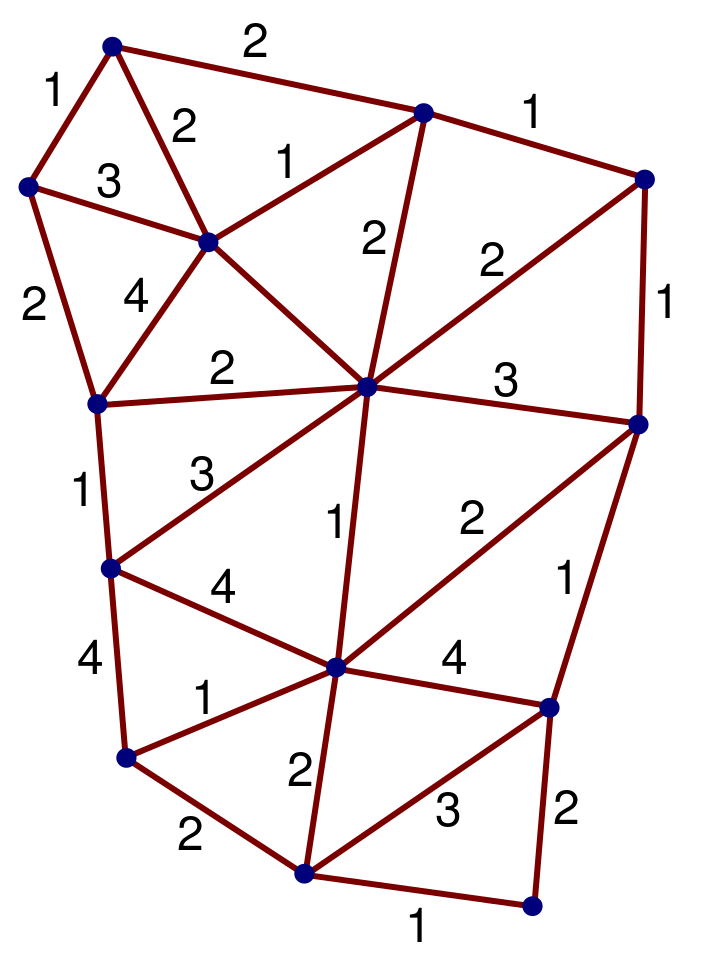
1971年，羅傑·彭羅斯提出一種圖形表示法，其中每個線段代表一個“單元”（基本粒子或粒子的複合系統）之世界線。三條線段匯聚在一個頂點。頂點可以詮釋為一個事件；在此事件中，一個單元分裂成兩個單元，或兩個單元碰撞合而為一。當一圖表中所有的線段都在頂點會合，則此圖為“封閉自旋網路”。時間以單一方向行進，比如從圖的底部走到圖的頂部。然而在封閉自旋網路的例子，時間行進的方向對於計算不構成影響。

每一線段標上一個稱作自旋量子數的整數。帶有自旋數n的一個單元稱作n-單元，其角動量為nħ，ħ是約化普朗克常數。光子、膠子等玻色子，其n為偶數；電子、夸克等費米子，其n為奇數。

給定一封閉自旋網路，則可計算出一個相應的非負整數的範數（norm）。範數可用來計算不同自旋值的機率。當一個自旋網路的範數是零，則其發生機率為零。當範數不為零時，在頂點處則有一些約束條件如下：

若有三個單元會合在一頂點，這三單元分別帶有自旋量子數a、b、c，則必須滿足

• 三角不等式：a必須小於或等於b+c，b必須小於或等於a+c，以及c必須小於或等於a+b。
• 費米子守恆（Fermion conservation）：a+b+c必須是偶數。

舉例來說，a= 3,b= 4,c= 6的例子是不可能，因為3 + 4 + 6 = 13是奇數。a= 3,b= 4,c= 9也不可能，因為3 + 4 < 9。而a= 3,b= 4,c= 5則可行，因為3 + 4 + 5 = 12是偶數且滿足三角不等式。

一些標記習慣會將整數標為半整數，約束條件則變成a+b+c的和要是整數。