基本介紹
- 中文名:自回歸滑動平均模型
- 外文名:Auto-Regressive Moving Average Model
- 別稱:ARMA模型
- 提出時間:20世紀70年代
- 提出人:金肯(JenKins)和波克斯(Box)
- 學科:數理科學
ARMA模型簡述
模型形式
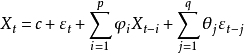
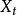
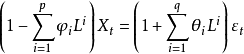

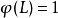

模型含義
識別條件
模型階數
模型參數最大似然估計時

模型參數最小二乘估計時
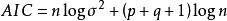
式中:n為樣本數,
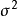
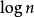

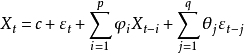
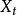
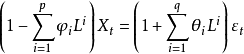

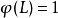


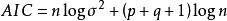
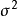
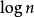
自回歸滑動平均模型,又名ARMA模型(Auto-Regressive Moving Average Model)。屬於時間序列分析中的一種,20世紀70年代,由美國統計學家金肯(JenKins)和波克斯(Box)提出...
求和自回歸滑動平均模型(integrated autore-gressive moving average model)簡稱ARIMA模型一種非平穩時間序列模型.如果時間序列.}}(t=0,士1, ...)是有一定增長...
ARIMA模型(英語:Autoregressive Integrated Moving Average model),差分整合移動平均自回歸模型,又稱整合移動平均自回歸模型(移動也可稱作滑動),時間序列預測分析方法之...
自回歸滑動平均模型(英語:Autoregressive moving average model,簡稱:ARMA模型)。是研究時間序列的重要方法,由自回歸模型(簡稱AR模型)與移動平均模型(簡稱MA模型)為...
對於短的或簡單的時間序列,可用趨勢模型和季節模型加上誤差來進行擬合。對於平穩時間序列,可用通用ARIMA模型(自回歸滑動平均模型)及其特殊情況的自回歸模型、滑動平均...
6.3.2 空間變化的混合多尺度自回歸預報模型的估計理論6.3.3 空間變化的混合多尺度自回歸預報模型的套用6.4 空間變化的混合多尺度自回歸滑動平均模型與套用...
式中X(Z)為輸出信號的Z變換,U(Z)為輸入信號的Z變換,以①式表達的信號模型稱為ARMA模型或稱為自回歸滑動平均模型。一旦確定了ARMA(P,M)模型的參數,就可得到...
ARMA 模型(Auto-Regressive and Moving Average Model)是研究時間序列的重要方法,由自回歸模型(簡稱AR模型)與滑動平均模型(簡稱MA模型)為基礎“混合”構成。...
給出了兩種用數字方法實現濾波器的過程.文獻建立了滿足一定功率譜密度特性的自回歸滑動平均風速模型,並對該模型的仿真結果進行了分析和對比。這些模型考慮了風電場內...
對於短的或簡單的時間序列,可用趨勢模型和季節模型加上誤差來進行擬合。對於平穩時間序列,可用通用ARMA模型(自回歸滑動平均模型)及其特殊情況的自回歸模型、滑動平均...
對於短的或簡單的時間序列,可用趨勢模型和季節模型加上誤差來進行擬合。對於平穩時間序列,可用通用ARMA模型(自回歸滑動平均模型)及其特殊情況的自回歸模型、滑動平均...
對於短的或簡單的時間序列,可用趨勢模型和季節模型加上誤差來進行擬合。對於平穩時間序列可用通用線性隨機模型(自回歸聯合滑動平均模型)及其特殊情況的自回歸模型、滑動...
7.2自回歸模型282 7.3滑動平均模型300 7.4自回歸滑動平均模型308 第8章平穩時間序列的模型擬合317 8.1自回歸模型擬合317 8.2滑動平均模型擬合329 8.3自回歸滑...
E3偏最小二乘回歸附錄F大氣變數時域分析F1自回歸模型F2滑動平均模型F3自回歸滑動平均模型F4方差分析模型F5均生函式模型F6經驗模態分解...
第二節 自回歸模型第三節 滑動平均模型第四節 自回歸滑動平均模型第五節 時間序列模型預測第六節 時間序列的套用第八章 非平穩經濟變數分析...
7.1基本內容211 7.2基本要求221 7.3習題詳解221 7.3.1時間序列概念221 7.3.2自回歸模型223 7.3.3滑動平均模型224 7.3.4自回歸滑動平均"[1] 參考...
ARMA譜估計,線性系統可以用線性差分方程進行描述,這種差分模型就是自回歸---滑動平均模型(AutoRegression---Moving Average,ARMA )。...
水文時間序列分析的內容包括對各種常用模型的介紹以及對建模型步驟的討論。常用的模型有自回歸模型(AR)、滑動平均模型(MA)、自回歸滑動平均混合模型(ARMA)、 自回歸...
在這個方案中,用一個表示輸入輸出關係的線性差分方程(可以包含干擾項)作為系統的預測數學模型(稱為可控自回歸滑動平均模型,縮寫為CARMA),用遞推最小二乘法線上...
SARIMA模型(Seasonal Autoregressive Integrated Moving Average),季節性差分自回歸滑動平均模型,時間序列預測分析方法之一。 ...
