基本介紹
結構力學簡介
工作任務
發展簡史

學科體系

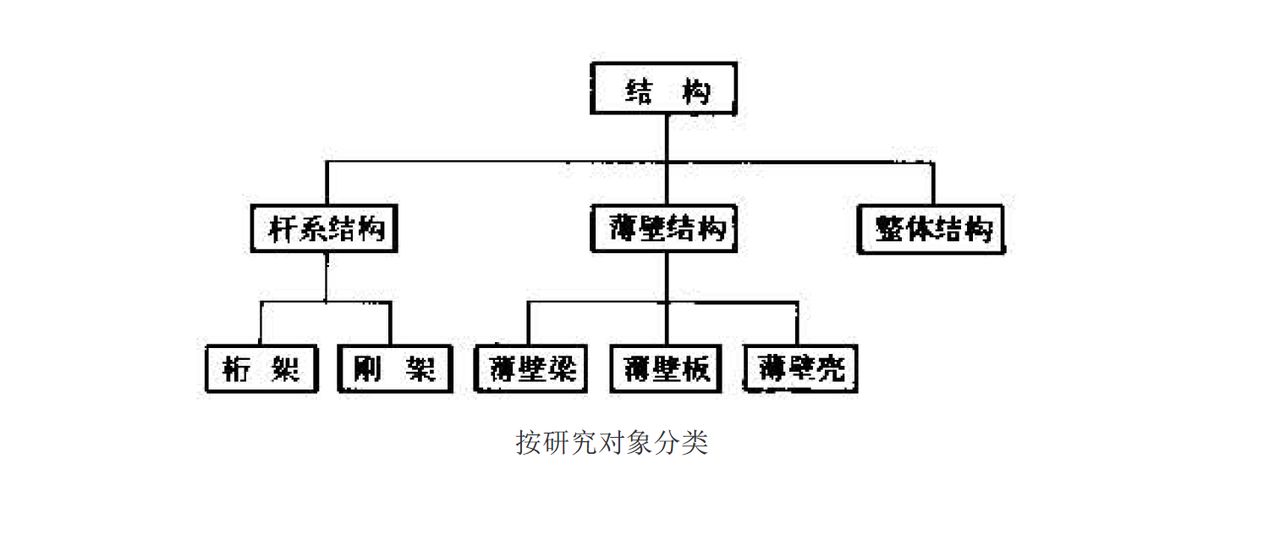




結構力學是固體力學的一個分支,它主要研究工程結構受力和傳力的規律,以及如何進行結構最佳化的學科,它是土木工程專業和機械類專業學生必修的學科。結構力學研究的內容...
《結構力學》是2008年清華大學出版社出版的圖書,作者是劉世奎。分為平面體系的幾何組成分析、靜定結構的概念及靜定梁、靜定平面剛架、結構位移計算、超靜定結構的...
《"十二五"普通高等教育本科國家級規劃教材·面向21世紀課程教材·結構力學1——基本教程(第3版)》是在第1版(面向21世紀課程教材,2002年全國普通高等學校優秀教材...
《結構力學(上)》是由武漢理工大學出版社於2012年出版的大學教材及工程參考書籍。...... 《結構力學(上)》是由武漢理工大學出版社於2012年出版的大學教材及工程參...
《結構力學》是2012年3月16日北京大學出版社出版的圖書,作者是邊亞東。...... 《結構力學》是2012年3月16日北京大學出版社出版的圖書,作者是邊亞東。 [1] ...
《結構力學》是2010年高等教育出版社出版圖書。...... 《結構力學(第5版)(上冊)》是普通高等教育“十一五”國家級規劃教材,是在第4版的基礎上,根據教育部高等學...
《結構力學(第2版)》作者王煥定,祁皚 。平裝。定價38元。...... 本書可作為高等學校土木、交通、水利等專業的結構力學教材,也可作為專升本、本科自考和相關專業工...
《結構力學(第二版)》是2014年9月1日中國電力出版社出版的一本圖書,作者是於玲玲、楊正光。...
《結構力學》是2016年北京大學出版社出版的圖書,作者是何春保 。...... 結構力學 書號: 27053 ISBN: 978-7-301-27053-0 作者: 何春保 版次: 1 開本: 16開...
《分析結構力學》是一本丁聖果編寫,由貴州科技出版社在2010年出版的書籍。...... 《定性結構力學》,二為計算結果數值化,即《程式結構力學》,目前雖然這樣的書還未...
《結構力學》是由作者王煥定編寫的一本基礎力學圖書,由清華大學出版社出版圖書。...... 《結構力學》是由作者王煥定編寫的一本基礎力學圖書,由清華大學出版社出版圖書...
以廣義力為未知量求解靜不定結構問題的一種方法。由於靜不定結構具有多餘約束,其廣義未知力不能單由平衡條件求出。...
《結構力學2:專題教程(第2版)》是2006年12月高等教育出版社出版的圖書,作者是龍馭球。主要講述了靜定結構總論、超靜定結構總論、能量原理、結構動力計算續論、...
本書是根據教育部頒布實施的《普通高等學校本科專業目錄》中規定的土木工程專業的培養目標和教育部高等學校力學基礎課程教學指導分委員會指定的《結構力學課程教學基本...
由陳建偉、武春廷、車文鵬等編寫,清華大學出版社出版。本書為《結構力學》(上冊),共10章,主要內容包括平面體系的幾何組成分析、靜定結構受力分析、靜定結構的...
《高等學校教材:結構力學》是1994年3月1日高等教育出版社出版的圖書,作者是龍馭球 包世華。...
本書按照《高等學校土木工程本科指導性專業規範》編寫,除緒論外共分11章,主要內容包括平面體系的幾何構造分析、靜定結構受力分析、虛功原理與結構的位移計算、力法...
《結構力學》是2005年化學工業出版社出版的圖書,作者是吳大煒。...... 結構力學內容簡介 編輯 全書共十章,分為緒論、結構的幾何組成分析、靜定結構的受力分析、靜...
結構動力學是研究結構在動力荷載作用下的振動問題。在動力荷載作用下,其一要考慮慣性力影響,其二考慮位移、內力、速度、加速度均隨時間變化而變化。...
《結構力學基礎》是在2001年由西北工業大學出版社出版的一部圖書,作者是黃其青。...... 《結構力學基礎》是在2001年由西北工業大學出版社出版的一部圖書,作者是黃...
《結構力學(下冊)》是2016年清華大學出版社出版的圖書,作者是潘旦光。...... 《結構力學(下冊)》是2016年清華大學出版社出版的圖書,作者是潘旦光。 [1] ...
《結構力學I》是2006年高等教育出版社出版的圖書,作者是袁駟。本書主要講述了靜定結構分析、超靜定結構分析、矩陣位移法、動力計算基礎等。...
《矩陣結構力學》是1997年中國建築工業出版社出版的圖書,作者是呂子華、呂令毅。...... 《矩陣結構力學》是1997年中國建築工業出版社出版的圖書,作者是呂子華、呂令毅...
本教材是根據國家教委批准試行的高等院校結構力學教學基本要求編寫而成的,為結構系列教材之一,分上、下兩冊出版。下冊內容包括:位移法、矩陣位移法、逐次漸近法和...
《02393 結構力學(一)》是2011年9月北京大學出版社出版的圖書,作者是中國就業培訓技術指導中心組織。...
《結構力學精講及真題祥解》是2010年中國建築工業出版社出版的圖書。...... 《結構力學精講及真題祥解》是2010年中國建築工業出版社出版的圖書。 [1] ...
《結構力學上》是2006年天津大學出版社出版的圖書,作者是劉昭培,張韞美。...... 《結構力學上》是2006年天津大學出版社出版的圖書,作者是劉昭培,張韞美。...
本書是以工科大學本科生為對象的工程力學教科書,其內容包括了材料力學、結構力學、彈性與塑性力學、能量法及有限元法、振動理論及地震回響分析、建築結構的設計等。...
《結構力學(第5版)(上冊)》是2010年高等教育出版社出版的圖書。本書主要介紹了平面體系的機動分析、靜定梁與靜定剛架、靜定拱等內容。...
飛機結構力學(structural mechanics of aircraft),是研究飛機結構在載荷和環境作用下的應力、變形、穩定性及其合理性的學科,又稱飛機結構理論,有時也稱為飛機強度學...
