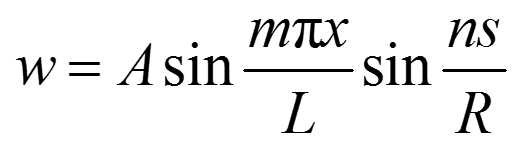研究簡史
平板的穩定性問題是G.H.布賴恩1891年首先進行論述的。他還用能量準則探討了加勁板(見加勁板殼)受純壓的穩定性問題。以後,S.P.鐵木辛柯根據隨遇平衡的概念,藉助彈性勢能的變分來求臨界壓力。圓筒殼的彈性穩定性問題是從20世紀初開始研究的。W.弗呂格等人用殼體變形的小撓度理論求得圓筒殼軸壓臨界值。以後,匈牙利的T.von卡門和中國的錢學森又提出了非線性"跳躍理論"。M.施泰因等人在1962年以後的數年中研究了非線性前屈曲性能及其對於屈曲方程和臨界壓力的影響,他的研究成果肯定了小撓度理論的價值。
實際工程殼體中總存在缺陷,如波形缺陷和滑型缺陷等,它們都會影響穩定性。學者們在研究初始缺陷的基礎上提出初始缺陷理論。這一理論可以較好地解釋實際失穩臨界值低於理論值這一現象。荷蘭的W.T.科伊特在1945年提出非完善結構的穩定性準則,引出"初始缺陷敏感度"的概念。他的理論將缺陷敏感度與理想的完善結構的初始後屈曲性能聯繫起來,因而叫作初始後屈曲理論。這是一個普遍的非線性理論,包括判斷臨界點穩定性的充分和必要條件。
板殼的平衡和穩定
一個在上下兩邊作用著壓力 σ的薄板或薄筒殼,在壓力比較小時,其內部產生壓應力和相應的壓應變,而不產生側向撓度ω。該板或殼由原來的不受力狀態轉為一個受力的平衡狀態。給這一平衡狀態以小干擾,比如給一個小的側向撓度,板或殼中就會產生相應於干擾的應力和應變。在干擾消除後,因干擾引起的應力和應變立刻消失並使板或殼恢復到受干擾前的狀態,因而稱開始的受力平衡狀態為穩定平衡狀態。如使σ不斷增加並大於某一數值後,干擾所引起的小撓度將迅速擴大,板殼受力的這種平衡稱為不穩定平衡。如果板殼所承受的外載荷從小值逐漸增大,則板殼將由穩定平衡過渡到不穩定平衡,在兩種平衡之間存在著一種過渡狀態,稱為臨界狀態,或稱隨遇平衡狀態。這一狀態所對應的外載荷稱為臨界載荷,其大小稱為臨界值,板殼內的相應應力稱為臨界應力,記為σcr 。失穩臨界應力值與結構的構造形式、邊界條件、材料性能、載荷大小及分布情況等多種因素有關。在結構設計中,應保證結構內的應力不超過臨界值。
失穩形態
板殼的失穩形態基本上分為分支點失穩和極值點失穩兩類。它們分別可用描述板殼中應力σ 和側向撓度w之間關係的圖1和圖2表示。分支點失穩的特徵是在板殼穩定平衡狀態I(圖1中曲線OA)附近存在另一個相鄰的勢能更小的平衡狀態Ⅱ(曲線AD),而在分支點A處發生兩種穩定性的轉換,板殼中的應力與撓度的關係由實曲線OAD表示;極值點失穩沒有上述的分支點,而板殼承載能力有一個最大的限度,壓力達到這個限度,板殼的承載能力就突然下降並伴隨出現較大變形(圖2)。與分支點和極值點相應的壓力值都稱為板殼的臨界壓力或臨界載荷,板殼中相應的壓應力為臨界應力。無論板還是殼,只要存在某種初始缺陷,一般來說,其失穩狀態多數是極值點失穩,有時失穩問題轉化為板殼的彎曲問題。
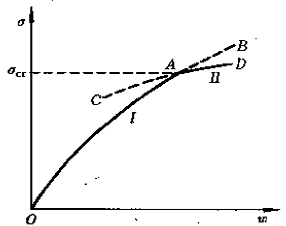 圖1 分支點失穩
圖1 分支點失穩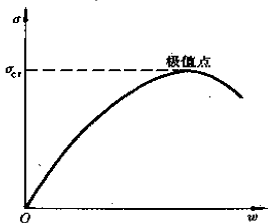 圖2 極值點失穩
圖2 極值點失穩穩定性理論和研究方法
穩定性理論和研究方法研究穩定性問題的理論可分為兩類:一類是經典線性理論,即小撓度理論,其中的應變-位移和應力-應變之間都是線性關係。另一類是非線性理論,也叫大撓度理論,其中的應變-位移關係和應力-應變關係兩者至少有一種是非線性的,前者的非線性稱為幾何非線性,後者的非線性稱為物理非線性。板殼在彈性狀態下的失穩問題一般是幾何非線性問題。若在失穩前已出現塑性變形,則失穩問題中物理非線性和幾何非線性一般是並存而且相互影響的。對於薄板,線性理論所計算出的臨界壓力值相當準確。對於殼體,實際臨界壓力值比用線性理論計算出的值要小,而且數值也很分散。在研究初始缺陷對失穩影響的基礎上發展起來的初始缺陷理論,能很好地解釋理論和實際間的差異。
在板殼穩定性問題中,最重要的內容是確定失隱臨界壓力,方法有三種:①靜力學方法:列出微擾動的平衡微分方程,將問題歸結為微分方程的本徵值問題,求出本徵值便可確定臨界壓力;②動力學方法:利用受微擾動後位移和位移速度不超出預先規定的界限的條件確定臨界壓力;③能量方法:利用勢能最小值條件確定臨界壓力。
常見的板殼穩定性問題板和殼的形式是多種多樣的,有平板、曲板、扁殼、圓筒殼、圓錐殼和各種形式的旋轉殼。它們所承受載荷的形式不盡相同,有單向受壓和雙向受壓,軸壓和外壓等。工程上最常見的皺損問題有:
① 平板的皺損 矩形平板在自身平面內沿一對邊均勻受壓下的臨界壓力公式為:
式中b為垂直於壓力方向的板寬;K為係數,隨板長、板寬和邊界條件的變化而變化,對於四邊簡支方板,K=4;D=E
/12(1-n)為彎曲剛度,式中t為板厚,E為材料的彈性模量,v為泊松比。實驗表明,在側向撓度較小時,上述板的臨界應力公式是相當準確的。當側向撓度達到一定值後,實際臨界應力要高於上述理論計算值。
 圖3 圓筒殼失穩後的撓度變化示意圖
圖3 圓筒殼失穩後的撓度變化示意圖②圓筒殼的皺損 一個半徑為R、長度為L、壁厚為t、兩端簡支的圓筒殼,在受軸向壓力作用而失穩後,其撓度可表示為:
式中x和s分別表示沿圓筒母線和周線方向的坐標;m為沿母線出現的半波數,2n為沿周向出現的半波數,m和n均與圓筒殼的尺寸有關。上式表示的撓度變化情況可見圖3。根據小撓度理論所計算出的臨界應力為:
式中K為常數,其理論值為0.605,但實驗表明實際的K值為理論值的1/5~1/2。薄殼的非線性理論就是在研究這種差異的背景下產生的。
③旋轉殼體的皺損 學者們除研究板和圓筒殼外,還研究圓錐殼、截錐殼、球形殼、橢球殼等旋轉殼體的穩定性,並得出臨界應力的計算公式。這些公式多數是根據線性理論求出結果,再按照實際數據加以修正,以供工程技術人員使用。
 圖1 分支點失穩
圖1 分支點失穩 圖2 極值點失穩
圖2 極值點失穩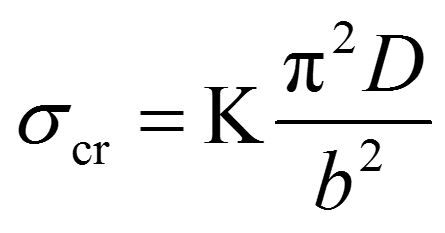
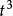
 圖3 圓筒殼失穩後的撓度變化示意圖
圖3 圓筒殼失穩後的撓度變化示意圖